题目内容
已知:对任意正实数x, 恒成立,则a的取值范围是:________.
恒成立,则a的取值范围是:________.
(-∞,2)
分析:令t=x+ ,则由基本不等式可得t=x
,则由基本不等式可得t=x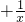
 可求t的最小值,对任意正实数x,
可求t的最小值,对任意正实数x, 恒成立,则a<tmin可求a
恒成立,则a<tmin可求a
解答:令t=x+ ,则由基本不等式可得t=x
,则由基本不等式可得t=x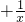
 =2
=2
当且仅当x= 即x=1时,t有最小值2
即x=1时,t有最小值2
∵对任意正实数x, 恒成立,则a<tmin=2
恒成立,则a<tmin=2
∴a<2
故答案为(-∞,2)
点评:本题主要考查了由函数的恒成立问题求解参数的取值范围,一般情况下a<f(x)(或a>f(x))恒成立a<f(x)min,(或a>f(x)max),解答本题的关键是利用基本不等式求解出函数的最小值
分析:令t=x+
 ,则由基本不等式可得t=x
,则由基本不等式可得t=x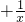
 可求t的最小值,对任意正实数x,
可求t的最小值,对任意正实数x, 恒成立,则a<tmin可求a
恒成立,则a<tmin可求a解答:令t=x+
 ,则由基本不等式可得t=x
,则由基本不等式可得t=x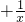
 =2
=2当且仅当x=
 即x=1时,t有最小值2
即x=1时,t有最小值2∵对任意正实数x,
 恒成立,则a<tmin=2
恒成立,则a<tmin=2∴a<2
故答案为(-∞,2)
点评:本题主要考查了由函数的恒成立问题求解参数的取值范围,一般情况下a<f(x)(或a>f(x))恒成立a<f(x)min,(或a>f(x)max),解答本题的关键是利用基本不等式求解出函数的最小值

练习册系列答案
相关题目
 对任意正实数x,y恒成立,则正实数
对任意正实数x,y恒成立,则正实数 的最小值是________
的最小值是________ 对任意正实数x,y恒成立,则正实数a的最小值为( )
对任意正实数x,y恒成立,则正实数a的最小值为( ) 对任意正实数x,y恒成立,则正实数a的最小值为 .
对任意正实数x,y恒成立,则正实数a的最小值为 . 对任意正实数x,y恒成立,则正实数a的最小值为 .
对任意正实数x,y恒成立,则正实数a的最小值为 .