题目内容
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD的动点,且 。
。
 。
。 
(1)求证:不论 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;
(2)当 为何值时,平面BEF⊥平面ACD。
为何值时,平面BEF⊥平面ACD。
 为何值,总有平面BEF⊥平面ABC;
为何值,总有平面BEF⊥平面ABC;(2)当
 为何值时,平面BEF⊥平面ACD。
为何值时,平面BEF⊥平面ACD。 (1)证明:∵∠BCD=90°,
∴BC⊥CD,
又∵AB⊥平面BCD,
∴AB⊥CD,
∴CD⊥平面ABC,
又∵ ,
,
∴EF∥CD,
∴EF⊥平面ABC,
∴平面BEF⊥平面ABC,
所以,不论 为何值,总有平面BEF⊥平面ABC。
为何值,总有平面BEF⊥平面ABC。
(2)解:由(1)EF⊥平面ABC,而BE 平面ABC,
平面ABC,
∴EF⊥BE,
又∵平面BEF⊥平面ACD,平面BEF 平面ACD=EF,
平面ACD=EF,
∴BE⊥平面ACD,
∴BE⊥AC,
∵∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,

BE= ,
,
∴AE= ,
,
∴ 。
。
∴BC⊥CD,
又∵AB⊥平面BCD,
∴AB⊥CD,
∴CD⊥平面ABC,
又∵
 ,
,∴EF∥CD,
∴EF⊥平面ABC,
∴平面BEF⊥平面ABC,
所以,不论
 为何值,总有平面BEF⊥平面ABC。
为何值,总有平面BEF⊥平面ABC。 (2)解:由(1)EF⊥平面ABC,而BE
 平面ABC,
平面ABC,∴EF⊥BE,
又∵平面BEF⊥平面ACD,平面BEF
 平面ACD=EF,
平面ACD=EF,∴BE⊥平面ACD,
∴BE⊥AC,
∵∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,

BE=
 ,
,∴AE=
 ,
,∴
 。
。
练习册系列答案
相关题目
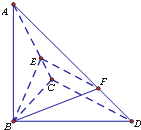 已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且
已知三棱锥A-BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E,F分别是直线AC,AD上的点,且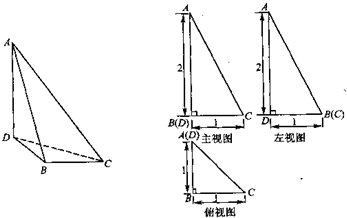 (2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.
(2009•大连一模)已知三棱锥A-BCD及其三视图如图所示.