题目内容
设两个非零向量a与b不共线,且ka+b与a+kb共线,则k的值为( )
| A.0 | B.1 | C.-1 | D.1或-1 |
D.
由题意,若两向量共线,则必存在常数λ,使得ka+b=λ(a+kb),
即(k-λ)a+(1-λk)b=0.,由于非零向量a与b不共线,
所以有k-λ=0且1-λk=0,解之得k=±1.
即(k-λ)a+(1-λk)b=0.,由于非零向量a与b不共线,
所以有k-λ=0且1-λk=0,解之得k=±1.

练习册系列答案
相关题目
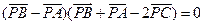 ,则△ABC一定为( )
,则△ABC一定为( )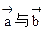 共线,
共线,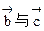 共线,则
共线,则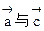 共线。
共线。 
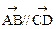 ,则
,则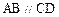 。
。 





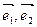 是不共线的向量,已知向量
是不共线的向量,已知向量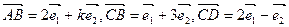 ,若A,B,D三点共线,求k的值
,若A,B,D三点共线,求k的值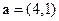 平移,则向量
平移,则向量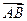 平移后的坐标是______________。
平移后的坐标是______________。 ,
, ,若
,若 ,则
,则
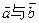 夹角为60°,
夹角为60°,