题目内容
抛物线Cl:y2=2x的焦点为F1,抛物线C2:x2=
y的焦点为F2,则过F1且与F1F2垂直的直线l的一般式方程为( )
| 1 |
| 2 |
分析:由抛物线的性质即可得出焦点,再利用相互垂直的直线斜率乘积等于-1即可得出斜率.
解答:解:由抛物线Cl:y2=2x的焦点为F1(
,0),由抛物线C2:x2=
y的焦点为F2(0,
).
∴kF1F2=
=-
.∴要求的直线的斜率为4.
∴过F1且与F1F2垂直的直线l的一般式方程为y-0=4(x-
),化为4x-y-2=0.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 8 |
∴kF1F2=
0-
| ||
|
| 1 |
| 4 |
∴过F1且与F1F2垂直的直线l的一般式方程为y-0=4(x-
| 1 |
| 2 |
故选C.
点评:熟练掌握抛物线的性质、相互垂直的直线斜率乘积等于-1等是解题的关键.

练习册系列答案
相关题目
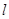 的一般方程式为
的一般方程式为