题目内容

函数y=
1-(
1
3
)2x-1
的定义域为
 
．
分析：欲求函数的定义域，即须被开方数要是非负数即可，即1-(
1
3
)2x-1≥0，由此即得所求的定义域．
解答：解：由1-(
1
3
)2x-1≥0得：
x≥
1
2
，
∴函数y=
1-(
1
3
)2x-1
的定义域为{x|x≥
1
2
}，
故答案为：{x|x≥
1
2
}．
点评：本题主要考查了函数的定义域及其求法，以及利用指数函数的性质求解不等式，属于基础题．
练习册系列答案
相关题目
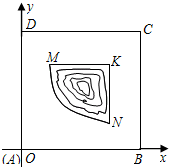（2011•徐州模拟）如图，某新建小区有一片边长为1（单位：百米）的正方形剩余地块ABCD，中间部分MNK是一片池塘，池塘的边缘曲线段MN为函数y=
2
9x
(
1
3
≤x≤
2
3
)的图象，另外的边缘是平行于正方形两边的直线段．为了美化该地块，计划修一条穿越该地块的直路（宽度不计），直路l与曲线段MN相切（切点记为P），并把该地块分为两部分．记点P到边AD距离为t，f（t）表示该地块在直路左下部分的面积．
（1）求f（t）的解析式；
（2）求面积S=f（t）的最大值．
已知函数y=（
1
3
）|x+1|，若曲线y=f（x）与直线y=b没有公共点，则b的取值范围是（　　）
函数y=log 
1
3
（1-3x）的定义域是（　　）
函数y=
1-(
1
3
)2x-1
的定义域为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网