Question

设数列{a_n}具有以下性质：①a₁=1；②当n∈N^*时，a_n≤a_n+1．
（Ⅰ）请给出一个具有这种性质的数列，使得不等式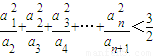对于任意的n∈N^*都成立，并对你给出的结果进行验证（或证明）；
（Ⅱ）若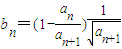，其中n∈N^*，且记数列{b_n}的前n项和B_n，证明：0≤B_n＜2．

Answer 1

【答案】分析：（I）令，则无穷数列{a_n}可由a₁=1，a_n+1=3^n-1a_n²（n≥1）给出，显然，该数列满足a₁=1，a_n≤a_n+1（n∈N^*），利用等比数列求和也满足条件；
（II）根据a_n≤a_n+1可得，∴b_n≥0，则B_n=b₁+b₂+…+b_n≥0，将转化成
，然后叠加可得结论．
解答：（Ⅰ）解：令，
则无穷数列{a_n}可由a₁=1，a_n+1=3^n-1a_n²（n≥1）给出．
显然，该数列满足a₁=1，a_n≤a_n+1（n∈N^*），
且------------------（6分）
（Ⅱ）证明∵，∴b_n≥0．
∴B_n=b₁+b₂+…+b_n≥0．-------------------------（8分）
又
=
=．
∴．
∴0≤B_n＜2．--------------------------------（14分）
点评：本题主要考查了数列与不等式的综合，以及数列的函数特性和求和，同时考查了转化的思想和计算能力，属于中档题．