Question

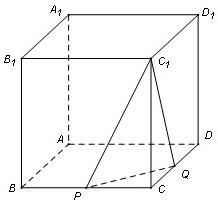如图，在正方体ABCD-A₁B₁C₁D₁中，P是棱BC的中点，Q在棱CD上．且DQ=λDC，若二面角P-C₁Q-C的余弦值为

14

7

，求实数λ的值．

Answer 1

分析：以A点为坐标原点，AB为x轴，AD为y轴，AA1为z轴，建立空间直角坐标系，设正方体的棱长为4，分别求出平面C₁PQ法向量和面C₁PQ的一个法向量，然后求出两法向量的夹角，建立等量关系，即可求出参数λ的值．

解答：解：以

AB

，

AD

，

AA1

为正交基底，
建立如图所示的空间直角坐标系A-xyz，
设正方体的棱长为4，则各点的坐标分别为
A（0，0，0），B（4，0，0），C（4，4，0），D（0，4，0）；
A₁（0，0，4），B₁（4，0，4），C₁（4，4，4），
D₁（0，4，4），P（4，2，0），Q（4λ，4，0）．（2分）
设平面C₁PQ法向量为

n

=(1，b，c)，
而

PC1

=(0，2，4)，

PQ

=(4λ-4，2，0)，
所以

2b+4c=0 (4λ-4)+2b=0

，
可得一个法向量

n

=(a，b，c)=（1，-2（λ-1），（λ-1）），（6分）
设面C₁PQ的一个法向量为

u

=(0，1，0)，
则|cos＜

n

，

u

＞|=|

-2(λ-1)

1+4(λ-1)2+(λ-1)2

|=

14

7

，（8分）
即：(λ-1)2=

1

9

，又因为点Q在棱CD上，所以λ=

2

3

．（10分）

点评：本题主要考查了二面角的度量，准确的建系，确定点坐标，熟悉向量的坐标表示，熟悉空间向量的计算在几何位置的证明，在有关线段，角的计算中的计算方法是解题的关键．