题目内容
已知α为锐角且 ,
,
(1)求tanα的值;
(2)求 的值.
的值.
(1) ,(2)
,(2) .
.
解析试题分析:(1)给值求值问题,关键研究角之间关系.本题只需展开即可. 由 展开得
展开得 ,解得tanα=
,解得tanα= ;(2)所求式子较复杂,需先化简.先统一角,
;(2)所求式子较复杂,需先化简.先统一角, =
= ,因此只需求
,因此只需求 的值即可.由同角三角函数关系得sinα=
的值即可.由同角三角函数关系得sinα= ,cosα=
,cosα= ,因此原式为
,因此原式为 .
.
试题解析:(1)∵
∴ ,即
,即 ,
,
解之得tanα= ;
;
(2)

∵α为锐角且tanα=
∴sinα= ,cosα=
,cosα= ,可得cosα+sinα=
,可得cosα+sinα= .
.
考点:两角和正切公式,同角三角函数关系,二倍角公式

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 .
. 的单调递增区间;
的单调递增区间; 是第二象限角,
是第二象限角, ,求
,求 的值.
的值. 中,
中,
 .
. 的值;
的值; 的值.
的值. ,且
,且 、
、 是方程
是方程 的两个根.
的两个根. 的值;
的值;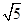 ,求△ABC的面积.
,求△ABC的面积. 的定义域为[
的定义域为[ ].
]. 的最小值.
的最小值. 中,
中, ,
, ,边
,边 的长为6,求角
的长为6,求角 大小及
大小及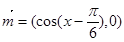 ,
,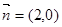 ,
,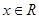 ,函数
,函数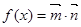 .
.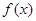 的表达式;
的表达式;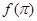 的值;
的值;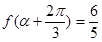 ,
,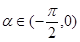 ,求
,求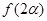 的值.
的值. 的三个内角A,B,C的对边,
的三个内角A,B,C的对边,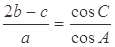
 时,求
时,求 的取值范围.
的取值范围.  ,x∈R,且
,x∈R,且 .
. ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.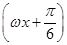 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π.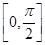 ,f
,f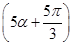 =-
=-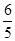 ,f
,f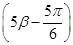 =
=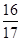 ,求cos(α+β)的值.
,求cos(α+β)的值.