题目内容
已知函数f(x)=x2-2x,集合M={(x,y)|f(x)+f(y)≤0},集合N={(x,y)|f(x)-f(y)≥0},则集合M∩N的面积是
- A.

- B.

- C.π
- D.2π
C
分析:因为f(x)=x2-2x,所以集合M={(x,y)|x2+y2-2x-2y≤0},它的图形是圆心为(1,1),半径为 的圆.N={(x,y)|x2-y2-2(x-y)≥0}={(x,y)|(x-y)(x+y-2)≥0},它的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的区域的面积是半径为
的圆.N={(x,y)|x2-y2-2(x-y)≥0}={(x,y)|(x-y)(x+y-2)≥0},它的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的区域的面积是半径为 的圆的面积的一半.由此能求出集合M∩N的面积.
的圆的面积的一半.由此能求出集合M∩N的面积.
解答: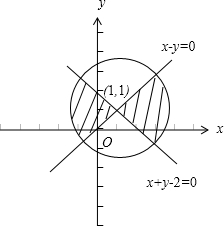 解:∵f(x)=x2-2x,
解:∵f(x)=x2-2x,
∴集合M={(x,y)|f(x)+f(y)≤0}
={(x,y)|x2+y2-2x-2y≤0},
集合M的图形是圆心为(1,1),半径为 的圆.
的圆.
N={(x,y)|f(x)-f(y)≥0}
={(x,y)|x2-y2-2(x-y)≥0}
={(x,y)|(x-y)(x+y-2)≥0},
集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.
∴集合M∩N的区域是如图所示的阴影部分.
它的面积是半径为 的圆的面积的一半.
的圆的面积的一半.
∴集合M∩N的面积S= =π.
=π.
故选C.
点评:本题考查圆和圆锥曲线的综合应用,解题的关键步骤是判断出集合M的图形是圆心为(1,1),半径为 的圆.集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的面积是半径为
的圆.集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的面积是半径为 的圆的面积的一半.解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.易错点是作不出来可行域,解题时要无从下手.
的圆的面积的一半.解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.易错点是作不出来可行域,解题时要无从下手.
分析:因为f(x)=x2-2x,所以集合M={(x,y)|x2+y2-2x-2y≤0},它的图形是圆心为(1,1),半径为
 的圆.N={(x,y)|x2-y2-2(x-y)≥0}={(x,y)|(x-y)(x+y-2)≥0},它的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的区域的面积是半径为
的圆.N={(x,y)|x2-y2-2(x-y)≥0}={(x,y)|(x-y)(x+y-2)≥0},它的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的区域的面积是半径为 的圆的面积的一半.由此能求出集合M∩N的面积.
的圆的面积的一半.由此能求出集合M∩N的面积.解答:
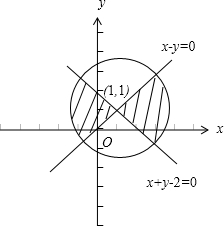 解:∵f(x)=x2-2x,
解:∵f(x)=x2-2x,∴集合M={(x,y)|f(x)+f(y)≤0}
={(x,y)|x2+y2-2x-2y≤0},
集合M的图形是圆心为(1,1),半径为
 的圆.
的圆.N={(x,y)|f(x)-f(y)≥0}
={(x,y)|x2-y2-2(x-y)≥0}
={(x,y)|(x-y)(x+y-2)≥0},
集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.
∴集合M∩N的区域是如图所示的阴影部分.
它的面积是半径为
 的圆的面积的一半.
的圆的面积的一半.∴集合M∩N的面积S=
 =π.
=π.故选C.
点评:本题考查圆和圆锥曲线的综合应用,解题的关键步骤是判断出集合M的图形是圆心为(1,1),半径为
 的圆.集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的面积是半径为
的圆.集合N的图形是直线x-y=0和直线x+y-2=0之间的平面区域.集合M∩N的面积是半径为 的圆的面积的一半.解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.易错点是作不出来可行域,解题时要无从下手.
的圆的面积的一半.解题时要认真审题,作出可行域,注意数形结合思想的灵活运用.易错点是作不出来可行域,解题时要无从下手. 
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|