题目内容
(本小题满分12分)在长方体 中,
中, ,
, .点
.点 是线段
是线段 上的动点,点
上的动点,点 为
为 的中点.
的中点.

(1)当 点是
点是 中点时,求证:直线
中点时,求证:直线 ∥平面
∥平面 ;
;
(2)若二面角 的余弦值为
的余弦值为 ,求线段
,求线段 的长.
的长.
【解析】
试题分析:第一步证明线面平行,有三种方法:1.判定定理,线线平行 线面平行;2.面面平行
线面平行;2.面面平行 线面平行;3.利用向量的方法证明),首选是线面平行的判定定理,按判定定理只需寻求线线平行,本题借助平行四边形去证.取
线面平行;3.利用向量的方法证明),首选是线面平行的判定定理,按判定定理只需寻求线线平行,本题借助平行四边形去证.取 的中点
的中点 ,连结
,连结 ,因
,因 分别是
分别是 的中点,
的中点, 为的中位线,则
为的中位线,则 ,又
,又 ,则
,则 ,得四边形
,得四边形 为平行四边形,则
为平行四边形,则 ,有了线线平行,自然就有线面平行了;第二步设
,有了线线平行,自然就有线面平行了;第二步设 ,建立空间直角坐标系,写出点
,建立空间直角坐标系,写出点 的坐标,先求平面
的坐标,先求平面 和平面
和平面 的法向量,然后借助二面角
的法向量,然后借助二面角 的余弦值为
的余弦值为 ,求线段
,求线段 的长
的长 即可.
即可.
试题解析:(1)证明:取 的中点
的中点 ,连结
,连结 ,
,

 ∥
∥ ,
, ∥
∥
 四边形
四边形 为平行四边形,可知
为平行四边形,可知 ∥
∥
 平面
平面 ,
, 平面
平面

 ∥平面
∥平面
(2)【解析】
设  ,如图建立空间直角坐标系
,如图建立空间直角坐标系
 ,
,

平面 的法向量为
的法向量为 ,由
,由 及
及 得
得
平面 的法向量为
的法向量为 , 由
, 由 及
及 得
得
 ,即
,即 
解得: 或
或 (舍去)
(舍去)
所以:
考点:1.线面平行的判定;2.利用法向量求二面角;
考点分析: 考点1:点、线、面之间的位置关系 考点2:异面直线所成的角 考点3:线面所成的角 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
 ,
, ,
, ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
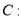
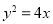 上一点
上一点 到
到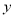 轴的距离为
轴的距离为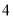 ,则点
,则点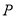 到抛物线
到抛物线 的焦点的距离是( )
的焦点的距离是( )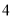 B.
B.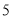 C.
C.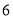 D.
D.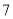
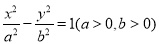 的一个焦点到一条渐近线的距离为
的一个焦点到一条渐近线的距离为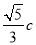 (
(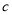 为双曲线的半焦距长),则该双曲线的离心率为( )
为双曲线的半焦距长),则该双曲线的离心率为( )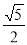 B.
B.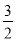 C.
C.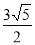 D.
D.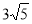
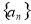 中,
中, 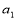 ,
,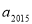 为方程
为方程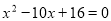 的两根,则
的两根,则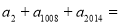 ( )
( ) 在点
在点 处的切线方程是
处的切线方程是 ;
; 的值域是
的值域是 ;
; ,其中
,其中 ,则
,则 ;
; 是
是 所在平面上一定点,动点P满足:
所在平面上一定点,动点P满足: ,
, ,则直线
,则直线 一定通过
一定通过 的内心;
的内心;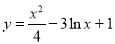 的一条切线的斜率为
的一条切线的斜率为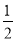 ,则切点的横坐标为( )
,则切点的横坐标为( )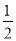
 ,
, 的夹角为
的夹角为 ,且
,且 ,
, ,则
,则
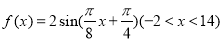 的图象与
的图象与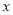 轴交于点
轴交于点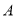 ,过点
,过点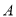 的直线
的直线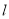 与函数
与函数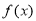 的图象交于
的图象交于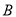 、
、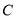 两点,
两点,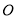 为坐标原点,则
为坐标原点,则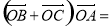 .
.