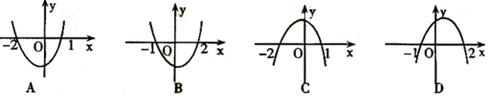题目内容
下列函数中,既是奇函数又是增函数的为
A. | B. | C. | D. |
D
解析试题分析:奇函数需要满足两个条件:1、定义域关于原点对称,2、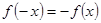
奇函数的性质:1、图像关于原点对称,2、关于观点对称的两个区间上函数图像的单调性相同,3、当函数在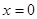 处有定义时,满足
处有定义时,满足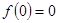 ,故可以首先排除A选择,其不是奇函数,而B选项是奇函数却是R上的减函数, C选项是奇函数,且在区间
,故可以首先排除A选择,其不是奇函数,而B选项是奇函数却是R上的减函数, C选项是奇函数,且在区间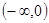 ,区间
,区间 上都单调增,但在整个定义域上不具有单调性,由排除法就可选出正确答案D,当然D选项可以转化成分段函数
上都单调增,但在整个定义域上不具有单调性,由排除法就可选出正确答案D,当然D选项可以转化成分段函数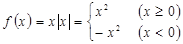 ,数形结合同样可以得到正确答案。
,数形结合同样可以得到正确答案。
考点:本题主要考查函数奇偶性的判断方法以及函数的单调性。
点评:本题学生可能忽略单调性的函数的局部性质这一特点,误选C项而造成失分。

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
已知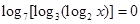 ,那么
,那么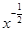 等于( )
等于( )
A.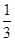 | B.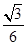 | C.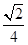 | D.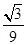 |
设函数
 的图象关于直线
的图象关于直线 及直线
及直线 对称,且
对称,且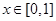 时,
时, ,则
,则 ( )
( )
A. | B. | C. | D. |
定义在R上的函数 满足
满足 ,且
,且
 .若当
.若当 时不等式
时不等式 成立,则
成立,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数 在(0,+∞)上( )
在(0,+∞)上( )
| A.既无最大值又无最小值 | B.仅有最小值 |
| C.既有最大值又有最小值 | D.仅有最大值 |
设偶函数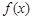 满足
满足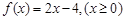 ,则不等式
,则不等式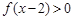 的解集是( )
的解集是( )
A.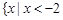 或 或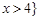 | B.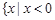 或 或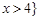 |
C.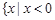 或 或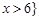 | D.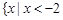 或 或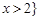 |
在下列函数中:①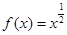 , ②
, ②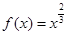 ,③
,③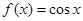 ,④
,④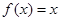 ,其中偶函数的个数是 ( )
,其中偶函数的个数是 ( )
| A.0 | B.1 | C.2 | D.3 |
 ;②
;② ;③
;③ ;④
;④ .则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是
.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是 
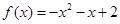 ,则函数
,则函数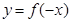 的图象为( )
的图象为( )