题目内容
定义在R上的函数
满足
，且
．若当
时不等式
成立，则
的取值范围是（ ）
A． | B． | C． | D． |
D
解析试题分析：由题意易知函数是定义在R上的奇函数且单调递增。因为时不等式成立，即
，所以
，画出可行域，得的取值范围是。
考点：本题考查函数的奇偶性、单调性、有关抽象函数的不等式的解法和线性规划的有关问题。
点评：本题以函数的单调性为载体，求解不等式恒成立时参数的取值范围，着重考查了函数单调性、二元二次不等式表示的平面区域等知识，较为综合，属于中档题．
练习册系列答案
相关题目
的图象只可能是 （ ）
下列函数中，在其定义域是减函数的是( )
A． | B． |
C． | D． |
函数
的定义域为
A． | B． | C． | D． |
下列函数中与函数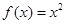
相等的是（ ）
A． | B． |
C． | D． |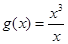
下列函数中，既是奇函数又是增函数的为
A． | B． | C． | D． |
函数
的单减区间是（ ）
A． | B． | C． | D． |
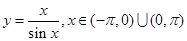的图象可能是下列图象中的 （ ）
的图象是曲线OAB，其中点O、A、B的坐标分别是（0,0），（1,2），（3,1），则
的值是