题目内容
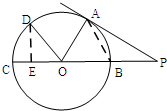 如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转600到OD,则PD的长为( )
如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转600到OD,则PD的长为( )分析:作DE⊥CB于E,根据题意先求得∠AOP=60°,∠DOC=60°.利用三角函数可求DE=
,EO=
.根据勾股定理即可求PD的值.
| ||
| 2 |
| 1 |
| 2 |
解答:解:如图,作DE⊥CB于E.

∵OB=PB=1,
∴OA=1.
又∵PA切⊙O于点A,
则OA⊥AP,
∴∠AOP=60°.
又∵OA绕点O逆时针方向旋转60°,
∴∠DOC=60°.
∴DE=1×sin60°=
,EO=
.
∴PD=
=
.
故选:D.

∵OB=PB=1,
∴OA=1.
又∵PA切⊙O于点A,
则OA⊥AP,
∴∠AOP=60°.
又∵OA绕点O逆时针方向旋转60°,
∴∠DOC=60°.
∴DE=1×sin60°=
| ||
| 2 |
| 1 |
| 2 |
∴PD=
(1+1+
|
| 7 |
故选:D.
点评:本题考点是与圆有关的比例线段,本题考查求线段的长度,平面几何中求线段长度一般在三角形中用正弦定理与余弦定理求解.

练习册系列答案
相关题目
 A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是
A.(不等式选讲选做题)函数y=|x+1|+|x-1|的最小值是 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为
A.若不等式|x-1|+|x-m|<2m的解集为∅,则m的取值范围为 到O D.
到O D.
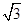 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.