题目内容
 选修4-1:几何证明选讲
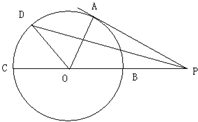
选修4-1:几何证明选讲如图,PA切圆O于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转60° 到OD.
(1)求线段PD的长;
(2)在如图所示的图形中是否有长度为
| 3 |
分析:(1)由PA与圆O相切,根据切线性质得到OA与AP垂直,所以三角形OPA为直角三角形,又B为斜边PO的中点,根据直角三角形斜边上的中线等于斜边的一半,得到AB=OB=OA,故三角形AOB为等边三角形,得到∠AOB=60°,由旋转角也为60°得到∠POD=120°,由OD及PO的长,利用余弦定理即可求出线段PD的长;
(2)线段PA长度为
,理由为:由PA为圆O的切线,PB为圆的割线,由切割线定理列出PA2=PB•PC,将PA和OB的长代入即可求出PA的长.
(2)线段PA长度为
| 3 |
解答:解:(1)∵PA切圆O于点A,∴OA⊥AP,即∠OAP=90°,
又B为PO中点,∴AB=OB=OA.
∴∠AOB=60°,∴∠POD=120°,
在△POD中,由OP=OB+PB=2,OD=1根据余弦定理得:
PD2=PO2+OD2-2PO•DOcos∠POD=7,
则PD=
;(5分)
(2)图形中有线段PA=
,理由如下:
∵PA是切线,PB=BO=OC
∴PA2=PB•PC=1×3=3,
∴PA=
.
又B为PO中点,∴AB=OB=OA.
∴∠AOB=60°,∴∠POD=120°,
在△POD中,由OP=OB+PB=2,OD=1根据余弦定理得:
PD2=PO2+OD2-2PO•DOcos∠POD=7,
则PD=
| 7 |
(2)图形中有线段PA=
| 3 |
∵PA是切线,PB=BO=OC
∴PA2=PB•PC=1×3=3,
∴PA=
| 3 |
点评:此题考查了切线的性质,余弦定理及切割线定理.要求学生掌握直线与圆相切时,圆心到切线的距离等于圆的半径,且圆的切线垂直于过切点的半径,熟练掌握余弦定理及切割线定理是解本题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲