题目内容
 在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE=![]() a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
a,BC=DE=a,∠EAB=∠ABC=∠DEA=90°.
(1)求证:PA⊥平面ABCDE;
(2)求二面角A-PD-E的大小;
(3)求点C到平面PDE的距离.
 (1)证明∵PA=AB=2a,PB=
(1)证明∵PA=AB=2a,PB=![]() a,
a,
∴PA2+AB2=PB2,∴∠PAB=90°,即PA⊥AB.
同理PA⊥AE.
∵AB∩AE=A,∴PA⊥平面ABCDE.
(2)解法一:∵∠AED=90°,
∴AE⊥ED.
∵PA⊥平面ABCDE,
∴PA⊥ED.
∴ED⊥平面PAE.
过A作AG⊥PE于G,
过DE⊥AG,
∴AG⊥平面PDE.
过G作GH⊥PD于H,连AH,
由三垂线定理得AH⊥PD.
∴∠AHG为二面角A-PD-E的平面角.
在直角△PAE中,AG=![]() a.
a.
在直角△PAD中,AH=![]() a,
a,
∴在直角△AHG中,sin∠AHG=![]() =
=![]() .∴∠AHG=arcsin
.∴∠AHG=arcsin![]() .
.
∴二面角A-PD-E的大小为arcsin![]() .
.
 解法二:建立如图所示的直角坐标系,
解法二:建立如图所示的直角坐标系,
则B(2a,0,0),E(0,2a,0),P(0,0,2a),D(a,2a,0),C(2a,a,0),
过A作AN⊥PD于N,
∵![]() =(a,2a,-2a),
=(a,2a,-2a),
设![]() =λ
=λ![]() ,
,
∴![]() =
=![]() +
+![]() =(λa,2λa,2a-2λa)
=(λa,2λa,2a-2λa)
∵AN⊥PD,
∴![]() ?
?![]() =0.
=0.
∴a?λa+2a?2λa-2a?(2a-2λa)=0.
解得λ=![]() .
.
∴![]() =(
=(![]() a,
a,![]() a,
a, ![]() a)
a)
即![]() =(-
=(-![]() a, -
a, -![]() a, -
a, -![]() a)
a)
同理,过E作EM⊥PD于M,
则![]() =(-
=(-![]() a,
a, ![]() a, -
a, -![]() a).
a).
二面角A-PD-E的大小为![]() ,
,![]() 所成的角<
所成的角<![]() ,
,![]() >.
>.
∵cos<![]() ,
,![]() >=arccos=
>=arccos=![]() .
.
∴<![]() ,
,![]() >=arccos=
>=arccos=![]() .
.
∴二面角A-PD-E的大小为arccos![]() .
.
 (3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
(3)解法一:∵∠EAB=∠ABC=∠DEA=90°,
BC=DE=a,AB=AE=2a,
取AE中点F,连CF,
∵AF∥=BC,
∴四边形ABCF为平行四边形.
∴CF∥AB,而AB∥DE,
∴CF∥DE,而DE![]() 平面PDE,CF
平面PDE,CF![]() 平面PDE,
平面PDE,
∴CF∥平面PDE.
∴点C到平面PDE的距离等于F到平面PDE的距离.
∵PA⊥平面ABCDE,
∴PA⊥DE.
又∵DE⊥AE,∴DE⊥平面PAE.
∴平面PAE⊥平面PDE.∴过F作FG⊥PE于G,则FG⊥平面PDE.
∴FG的长即F点到平面PDE的距离.
在△PAE中,PA=AE=2a,F为AE中点,FG⊥PE,
 ∴FG=
∴FG=![]() a. ∴点C到平面PDE的距离为
a. ∴点C到平面PDE的距离为![]() a.
a.
解法二:∵PA平面ABCDE,∴PA⊥DE,
又∵∠DEA=90°,∴DE⊥平面PAE,∴DE⊥PE.
∵BC=DE=a,AB=AE=2a,
连接CE,
则S△CDE=![]() a2,S△DEP=
a2,S△DEP=![]() a2 .
a2 .
∵VP-CDE=![]() ?PA?S△CDE=
?PA?S△CDE=![]() ?2a?
?2a?![]() a2=
a2=![]() a2.
a2.
设点C到平面PDE的距离为h,
则V C-PDE=![]() ?h?S△PDE=
?h?S△PDE=![]() ?h?
?h?![]() a2=
a2=![]() a2h.
a2h.
∵VP-CDE=VC-PDE,
即![]() a3=
a3=![]() a2h,
a2h,
解得h=![]() a.即点C到平面PDE的距离为
a.即点C到平面PDE的距离为![]() a.
a.
解法三:建立如图所示的直角坐标系,
 则B(2a,0,0),E(0,2a,0),P(0,0,2a),
则B(2a,0,0),E(0,2a,0),P(0,0,2a),
D(a,2a,0),C(2a,a,0),
设平面PDE的一个法向量为n=(x,y,1),
∵![]() =(0,2a,-2a),
=(0,2a,-2a),![]() =(-a,0,0),
=(-a,0,0),
又∵n⊥平面PDE.
∴n⊥![]() ,n⊥
,n⊥![]() .
.
∴
即![]()
解得![]()
∴n=(0,1,1).
∵![]() =(-a,a,0),
=(-a,a,0),
∴cos<![]() ,n>=
,n>=![]()
∵0≤<![]() ,n>≤π,
,n>≤π,
∴<![]() ,n>=
,n>=![]() .
.
∵过C作CH⊥平面PDE于H,则CH=|![]() |?|cos<
|?|cos<![]() ,n>|,
,n>|,
即点C到平面PDE的距离为
|![]() |?|cos<
|?|cos<![]() ,n>|=
,n>|=![]() a.
a.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案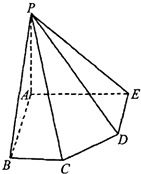
 四棱锥P-ABCD的三视图如图所示,四棱锥P-ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为
四棱锥P-ABCD的三视图如图所示,四棱锥P-ABCD的五个顶点都在一个球面上,E、F分别是棱AB、CD的中点,直线EF被球面所截得的线段长为 (2013•虹口区一模)在正四棱锥P-ABCD中,侧棱PA的长为
(2013•虹口区一模)在正四棱锥P-ABCD中,侧棱PA的长为
