题目内容
下列四个函数中(1)f(x)=cox2x-sin2x;(2)?(x)=x2•cscx(3)h(x)=tanx+sinx;(4)g(x)=1g(sinx+
)是奇函数的有( )
| 1+sin2x |
| A.1个 | B.2个 | C.3个 | D.4个 |
根据题意,四个函数的定义域都关于原点对称.
(1)定义域为R,f(-x)=cox2(-x)-sin2(-x)=f(x)偶函数;
(2)定义域为{x|x≠kπ,x∈R},?(-x)=(-x)2•csc(-x)=-(x2•cscx)=-f(x)是奇函数
(3)定义域为{x|x≠kπ+
,x∈R},h(-x)=tan(-x)+sin(-x)=-(tanx+sinx)=-f(x)是奇函数
(4)定义域为R,g(-x)=1g(sin(-x)+
)=-1g(sinx+
)是奇函数
故选C
(1)定义域为R,f(-x)=cox2(-x)-sin2(-x)=f(x)偶函数;
(2)定义域为{x|x≠kπ,x∈R},?(-x)=(-x)2•csc(-x)=-(x2•cscx)=-f(x)是奇函数
(3)定义域为{x|x≠kπ+
| π |
| 2 |
(4)定义域为R,g(-x)=1g(sin(-x)+
| 1+sin2x |
| 1+sin2x |
故选C

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
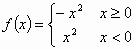 ,能被称为“理想函数”的有________(填相应的序号).
,能被称为“理想函数”的有________(填相应的序号). ,能被称为“理想函数”的有________(填相应的序号).
,能被称为“理想函数”的有________(填相应的序号). 是奇函数的有( )
是奇函数的有( )