题目内容
已知定点A(0,1)、B(0,-1)、C(1,0),动点P满足: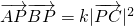 (k∈R).
(k∈R).
(1)求动点P的轨迹方程,并说明方程表示的图形;
(2)当k=2时,求 的最大值和最小值.
的最大值和最小值.
解:( 1 ) 设动点P的坐标为(x,y),则 ,
, ,
,
∵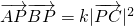 ,∴x2+y2-1=k[(x-1)2+y2],即(k-1)x2+(k-1)y2-2kx+k+1=0
,∴x2+y2-1=k[(x-1)2+y2],即(k-1)x2+(k-1)y2-2kx+k+1=0
若k=1,,则方程为x=1,表示过点(1,0)且平行于y轴的直线;
若k≠1,则方程为(x+ )2+y2=(
)2+y2=( )2,表示以(
)2,表示以( ,0)为圆心,以
,0)为圆心,以 为半径的圆;
为半径的圆;
( 2 ) 当k=2时,方程化为(x-2)2+y2=1, =|(2x,2y)|=2
=|(2x,2y)|=2
令x=2+cosθ,y=sinθ,则 =2
=2
∴当cosθ=1时, 的最大值为6,当cosθ=-1时,
的最大值为6,当cosθ=-1时, 的最小值为2.
的最小值为2.
分析:(1)根据题意,设出P的坐标(x,y),可得向量的坐标,代入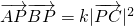 |中,可得(k-1)x2+(k-1)y2-2kx+k+1=0,分k=1与k≠1两种情况讨论,可得答案;
|中,可得(k-1)x2+(k-1)y2-2kx+k+1=0,分k=1与k≠1两种情况讨论,可得答案;
(2)表示出向量和的模,利用圆的参数方程设点的坐标,即可求得 的最大值和最小值.
的最大值和最小值.
点评:本题考查直线与圆的方程的综合运用,考查向量知识的运用,考查圆的参数方程,属于中档题.
 ,
, ,
,∵
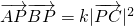 ,∴x2+y2-1=k[(x-1)2+y2],即(k-1)x2+(k-1)y2-2kx+k+1=0
,∴x2+y2-1=k[(x-1)2+y2],即(k-1)x2+(k-1)y2-2kx+k+1=0 若k=1,,则方程为x=1,表示过点(1,0)且平行于y轴的直线;
若k≠1,则方程为(x+
 )2+y2=(
)2+y2=( )2,表示以(
)2,表示以( ,0)为圆心,以
,0)为圆心,以 为半径的圆;
为半径的圆;( 2 ) 当k=2时,方程化为(x-2)2+y2=1,
 =|(2x,2y)|=2
=|(2x,2y)|=2
令x=2+cosθ,y=sinθ,则
 =2
=2
∴当cosθ=1时,
 的最大值为6,当cosθ=-1时,
的最大值为6,当cosθ=-1时, 的最小值为2.
的最小值为2.分析:(1)根据题意,设出P的坐标(x,y),可得向量的坐标,代入
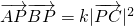 |中,可得(k-1)x2+(k-1)y2-2kx+k+1=0,分k=1与k≠1两种情况讨论,可得答案;
|中,可得(k-1)x2+(k-1)y2-2kx+k+1=0,分k=1与k≠1两种情况讨论,可得答案;(2)表示出向量和的模,利用圆的参数方程设点的坐标,即可求得
 的最大值和最小值.
的最大值和最小值.点评:本题考查直线与圆的方程的综合运用,考查向量知识的运用,考查圆的参数方程,属于中档题.

练习册系列答案
相关题目
 已知定点A(0,-1),点B在圆F:x2+(y-1)2=16上运动,F为圆心,线段AB的垂直平分线交BF于P.
已知定点A(0,-1),点B在圆F:x2+(y-1)2=16上运动,F为圆心,线段AB的垂直平分线交BF于P. (文科)已知定点A(0,-1),点M(x,y)在曲线y=x2(0<x<3)上运动,过点M作垂直于x轴的直线l,l交直线y=9于点N.
(文科)已知定点A(0,-1),点M(x,y)在曲线y=x2(0<x<3)上运动,过点M作垂直于x轴的直线l,l交直线y=9于点N.