Question

已知函数（a∈R）．

（1）试判断f（x）的单调性，并证明你的结论；

（2）若f（x）为定义域上的奇函数，

①求函数f（x）的值域；

②求满足f（ax）＜f（2a﹣x²）的x的取值范围．

Answer 1

考点：

函数单调性的判断与证明；函数的值域；函数单调性的性质；函数奇偶性的判断．

专题：

综合题；函数的性质及应用．

分析：

（1）函数f（x）为定义域（﹣∞，+∞），且，任取x₁，x₂∈（﹣∞，+∞），且x₁＜x₂，推导出f（x₂）﹣f（x₁）＞0，由此得到f（x）在（﹣∞，+∞）上的单调增函数．

（2）由f（x）是定义域上的奇函数，知对任意实数x恒成立，由此能够求出函数f（x）的值域和满足f（ax）＜f（2a﹣x²）的x的取值范围．

解答：

（本小题满分16分）

解：（1）函数f（x）为定义域（﹣∞，+∞），

且，

任取x₁，x₂∈（﹣∞，+∞），且x₁＜x₂

则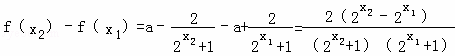…（3分）

∵y=2^x在R上单调递增，且x₁＜x₂

∴，，，，

∴f（x₂）﹣f（x₁）＞0，

即f（x₂）＞f（x₁），

∴f（x）在（﹣∞，+∞）上的单调增函数．…（5分）

（2）∵f（x）是定义域上的奇函数，∴f（﹣x）=﹣f（x），

即对任意实数x恒成立，

化简得，

∴2a﹣2=0，即a=1，…（8分）

（注：直接由f（0）=0得a=1而不检验扣2分）

①由a=1得，

∵2^x+1＞1，∴，…（10分）

∴，∴

故函数f（x）的值域为（﹣1，1）．…（12分）

②由a=1，得f（x）＜f（2﹣x²），

∵f（x）在（﹣∞，+∞）上单调递增，∴x＜2﹣x²，…（14分）

解得﹣2＜x＜1，

故x的取值范围为（﹣2，1）．…（16分）

点评：

本题考查函数的单调性的判断，考查函数的值域的求法和满足f（ax）＜f（2a﹣x²）的x的取值范围．解题时要认真审题，仔细解答，注意定义法判断函数的单调性的应用．