题目内容
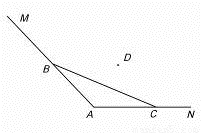
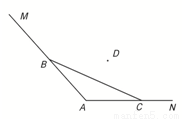
 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.(1)若BC=l,求养殖场面积最大值;
(2)若B、C为定点,BC<l,在折线MBCN内选点D,使BD+DC=l,求四边形养殖场DBAC的最大面积;
(3)若(2)中B、C可选择,求四边形养殖场ACDB面积的最大值.
分析:(1)先设AB=x,AC=y,x>0,y>0,由余弦定理得出关于x,y的等式,再结合基本不等式求出xy的最大值,从而得出养殖场面积最大值;
(2)设AB=m,AC=n(m,n为定值).由DB+DC=l=2a为定值知点D在以B、C为焦点的椭圆上,欲使四边形养殖场DBAC的最大面积,只需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点即可.
(3)先确定点B、C,使BC<l.由(2)知△DBC为等腰三角形时,四边形ACDB面积最大.确定△BCD的形状,使B、C分别在AM、AN上滑动,且BC保持定值,由(1)知AB=AC时,四边形ACDB面积最大.
(2)设AB=m,AC=n(m,n为定值).由DB+DC=l=2a为定值知点D在以B、C为焦点的椭圆上,欲使四边形养殖场DBAC的最大面积,只需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点即可.
(3)先确定点B、C,使BC<l.由(2)知△DBC为等腰三角形时,四边形ACDB面积最大.确定△BCD的形状,使B、C分别在AM、AN上滑动,且BC保持定值,由(1)知AB=AC时,四边形ACDB面积最大.
解答:解:(1)设AB=x,AC=y,x>0,y>0.l_=x_+y_-2xycos2θ≥2xy-2xycos2θ,xy≤
=
,S=
xysin2θ≤
•
•2sinθcosθ=
,
所以,△ABC面积的最大值为
,当且仅当x=y时取到.
(2)设AB=m,AC=n(m,n为定值). BC=2c(定值),
由DB+DC=l=2a,a=
l,知点D在以B、C为焦点的椭圆上,S△ABC=
mnsin2θ为定值.
只需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点.b=
=
,S△BCD面积的最大值为
•2c•b=c•
,
因此,四边形ACDB面积的最大值为
m•n•sin2θ+c•
.
(3)先确定点B、C,使BC<l.由(2)知△DBC为等腰三角形时,四边形ACDB面积最大.
确定△BCD的形状,使B、C分别在AM、AN上滑动,且BC保持定值,
由(1)知AB=AC时,四边形ACDB面积最大.
此时,△ACD≌△ABD,∠CAD=∠BAD=θ,且CD=BD=
.
S=2S△ACD=2•
•AC•AD•sinθ.
由(1)的同样方法知,AD=AC时,三角形ACD面积最大,最大值为
•
•
.
所以,四边形ACDB面积最大值为
.
| l2 |
| 2-2cos2θ |
| l2 |
| 4sin2θ |
| 1 |
| 2 |
| 1 |
| 2 |
| l2 |
| 4sin2θ |
| l2cosθ |
| 4sinθ |
所以,△ABC面积的最大值为
| l2cosθ |
| 4sinθ |
(2)设AB=m,AC=n(m,n为定值). BC=2c(定值),
由DB+DC=l=2a,a=
| 1 |
| 2 |
| 1 |
| 2 |
只需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点.b=
| a2-c2 |
|
| 1 |
| 2 |
|
因此,四边形ACDB面积的最大值为
| 1 |
| 2 |
|
(3)先确定点B、C,使BC<l.由(2)知△DBC为等腰三角形时,四边形ACDB面积最大.
确定△BCD的形状,使B、C分别在AM、AN上滑动,且BC保持定值,
由(1)知AB=AC时,四边形ACDB面积最大.
此时,△ACD≌△ABD,∠CAD=∠BAD=θ,且CD=BD=
| l |
| 2 |
S=2S△ACD=2•
| 1 |
| 2 |
由(1)的同样方法知,AD=AC时,三角形ACD面积最大,最大值为
| 1 |
| 2 |
| l |
| 2 |
| ||
tan
|
所以,四边形ACDB面积最大值为
| l2 | ||
8tan
|
点评:本小题主要考查余弦定理、基本不等式、椭圆的定义等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于中档题.

练习册系列答案
相关题目
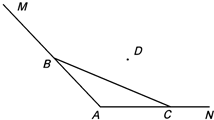 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.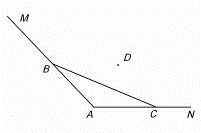 如图,海岸线MAN,
如图,海岸线MAN,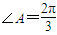 ,现用长为6的拦网围成一养殖场,其中B∈MA,C∈NA.
,现用长为6的拦网围成一养殖场,其中B∈MA,C∈NA.