题目内容
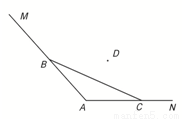
如图,海岸线MAN,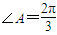 ,现用长为6的拦网围成一养殖场,其中B∈MA,C∈NA.
,现用长为6的拦网围成一养殖场,其中B∈MA,C∈NA.(1)若BC=6,求养殖场面积最大值;
(2)若AB=2,AC=4,在折线MBCN内选点D,使BD+DC=6,求四边形养殖场DBAC的最大面积(保留根号).
【答案】分析:(1)设AB为x,AC为y,根据BC=6, ,结合余弦定理及基本不等式可得xy的范围,代入三角形面积公式,可得养殖场面积最大值;
,结合余弦定理及基本不等式可得xy的范围,代入三角形面积公式,可得养殖场面积最大值;
(2)由AB=2,AC=4, ,结合余弦定理,可求出BC长,若四边形养殖场DBAC的最大面积,则△DBC面积最大即可,根据椭圆的定义及几何特征,D为以BC为焦点的椭圆的短轴顶点时满足条件.
,结合余弦定理,可求出BC长,若四边形养殖场DBAC的最大面积,则△DBC面积最大即可,根据椭圆的定义及几何特征,D为以BC为焦点的椭圆的短轴顶点时满足条件.
解答:解:(1)设AB=x,AC=y,x>0,y>0.
BC2=x2+y2-2xycos ≥2xy-2xy(-
≥2xy-2xy(- ),
),
∴xy≤12,
S= xysin
xysin ≤3
≤3
所以,△ABC面积的最大值为 3 ,当且仅当x=y时取到.
,当且仅当x=y时取到.
(2)∵AB=2,AC=4,
BC= =2
=2 ,
,
由DB+DC=6,知点D在以B、C为焦点的椭圆上,
∵S△ABC=2 为定值
为定值
只需故四边形养殖场DBAC的面积最大时,仅需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点,
S△BCD面积的最大值为 ,
,
因此,四边形ACDB面积的最大值为 2 +
+
点评:本题考查的知识点是解三角形的实际应用,余弦定理,椭圆的定义及几何性质,难度较大,属于难题.
 ,结合余弦定理及基本不等式可得xy的范围,代入三角形面积公式,可得养殖场面积最大值;
,结合余弦定理及基本不等式可得xy的范围,代入三角形面积公式,可得养殖场面积最大值;(2)由AB=2,AC=4,
 ,结合余弦定理,可求出BC长,若四边形养殖场DBAC的最大面积,则△DBC面积最大即可,根据椭圆的定义及几何特征,D为以BC为焦点的椭圆的短轴顶点时满足条件.
,结合余弦定理,可求出BC长,若四边形养殖场DBAC的最大面积,则△DBC面积最大即可,根据椭圆的定义及几何特征,D为以BC为焦点的椭圆的短轴顶点时满足条件.解答:解:(1)设AB=x,AC=y,x>0,y>0.
BC2=x2+y2-2xycos
 ≥2xy-2xy(-
≥2xy-2xy(- ),
),∴xy≤12,
S=
 xysin
xysin ≤3
≤3
所以,△ABC面积的最大值为 3
 ,当且仅当x=y时取到.
,当且仅当x=y时取到.(2)∵AB=2,AC=4,
BC=
 =2
=2 ,
,由DB+DC=6,知点D在以B、C为焦点的椭圆上,
∵S△ABC=2
 为定值
为定值只需故四边形养殖场DBAC的面积最大时,仅需△DBC面积最大,需此时点D到BC的距离最大,即D必为椭圆短轴顶点,
S△BCD面积的最大值为
 ,
,因此,四边形ACDB面积的最大值为 2
 +
+
点评:本题考查的知识点是解三角形的实际应用,余弦定理,椭圆的定义及几何性质,难度较大,属于难题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
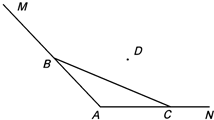 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.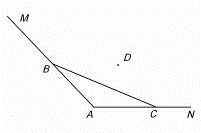 如图,海岸线MAN,
如图,海岸线MAN, 如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.
如图,海岸线MAN,∠A=2θ,现用长为l的拦网围成一养殖场,其中B∈MA,C∈NA.