题目内容
 如图F1,F2分别是椭圆
如图F1,F2分别是椭圆| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由题设条件知 A(-
,
),把A代入椭圆
+
=1(a>b>0),得
+
=1,整理,得e4-8e2+4=0,由此能够求出椭圆的离心率.
| c |
| 2 |
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| 4a2 |
| 3c2 |
| 4b2 |
解答:解:由题意知 A(-
,
),
把A代入椭圆
+
=1(a>b>0),得
+
=1,
∴(a2-c2)c2+3a2c2=4a2(a2-c2),
整理,得e4-8e2+4=0,
∴e2=
=4±2
,
∵0<e<1,∴e=
-1.
故选D.
| c |
| 2 |
| ||
| 2 |
把A代入椭圆
| x2 |
| a2 |
| y2 |
| b2 |
| c2 |
| 4a2 |
| 3c2 |
| 4b2 |
∴(a2-c2)c2+3a2c2=4a2(a2-c2),
整理,得e4-8e2+4=0,
∴e2=
8±
| ||
| 2 |
| 3 |
∵0<e<1,∴e=
| 3 |
故选D.
点评:本题考查椭圆的性质和应用,解题时要认真审题,注意公式的灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
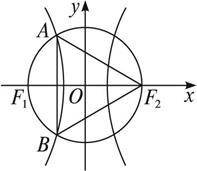
 的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )




 的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )




 的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )
的两个焦点,A和B是以O为圆心,以|OF1|为半径的圆与该左半椭圆的两个交点,且△F2AB是等边三角形,则椭圆的离心率为( )



