题目内容
若 (n∈N*),则
(n∈N*),则 =________.
=________.

分析:化简数列的通项,利用裂项法,求出数列的和,然后通过数列极限的运算法则,求出极限.
解答:因为
 ,
,所以

=
 +
+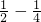 +
+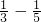

=
 .
.所以
 =
= =
= =
= .
.故答案为:
 .
.点评:本题考查数列通项公式的应用,裂项法求法数列的和,数列极限的应用,考查计算能力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知各项均不为零的数列{an},定义向量
=(an,an+1),
=(n,n+1),n∈N*.下列命题中真命题是( )
| cn |
| bn |
A、若?n∈N*总有
| ||||
B、若?n∈N*总有
| ||||
C、若?n∈N*总有
| ||||
D、若?n∈N*总有
|
设非空集合M同时满足下列两个条件:
①M⊆{1,2,3,…,n-1};
②若a∈M,则n-a∈M,(n≥2,n∈N+).
则下列结论正确的是( )
①M⊆{1,2,3,…,n-1};
②若a∈M,则n-a∈M,(n≥2,n∈N+).
则下列结论正确的是( )
A、若n为偶数,则集合M的个数为2
| ||
B、若n为偶数,则集合M的个数为2
| ||
C、若n为奇数,则集合M的个数为2
| ||
D、若n为奇数,则集合M的个数为2
|