题目内容
函数f(x)的定义域为R,并满足以下条件:
①对任意x∈R,有f(x)>0; ②对任意x、y∈R,有f(xy)=[f(x)]y; ③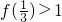 .
.
(1)求f(0)的值;
(2)求证:f(x)在R上是单调增函数;
(3)若f(2)=2,且x满足 ,求函数
,求函数 的最大值和最小值.
的最大值和最小值.
解:(1)令x=0,y=2,得:f(0)=[f(0)]2,∵f(0)>0,∴f(0)=1.
(2)任取x1,x2∈R,且x1<x2,设 ,
, ,则p1<p2,
,则p1<p2,
∴f(x1)-f(x2)=f( )-f(
)-f( )=
)=
∵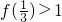 ,p1<p2,∴f(x1)<f(x2)
,p1<p2,∴f(x1)<f(x2)
∴f(x)在R上是单调增函数;
(3)由(2)及 知,
知,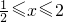 ,
,
又f(2log2x)= =
= =x,
=x,
于是y=2x+ =2(x+
=2(x+ )在[
)在[ ,
, ]上单调递减,在[
]上单调递减,在[ ,2]上单调递增,
,2]上单调递增,
f( )=3,f,2)=
)=3,f,2)= ,因此最大值为x=2时,y=
,因此最大值为x=2时,y= ,最小值为x=
,最小值为x= 时,y=2
时,y=2
综上所述, 的最大值为
的最大值为 ,,最小值为2
,,最小值为2
分析:(1)令x=0,y=2,代入可得答案;
(2)设 ,
, ,作差后由函数的性质可判单调性;
,作差后由函数的性质可判单调性;
(3)由(2)及已知条件化简所给函数,由函数的单调性可得最值.
点评:本题为抽象函数的综合应用,涉及函数的单调性和最值,属中档题.
(2)任取x1,x2∈R,且x1<x2,设
 ,
, ,则p1<p2,
,则p1<p2,∴f(x1)-f(x2)=f(
 )-f(
)-f( )=
)=
∵
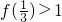 ,p1<p2,∴f(x1)<f(x2)
,p1<p2,∴f(x1)<f(x2)∴f(x)在R上是单调增函数;
(3)由(2)及
 知,
知,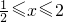 ,
,又f(2log2x)=
 =
= =x,
=x,于是y=2x+
 =2(x+
=2(x+ )在[
)在[ ,
, ]上单调递减,在[
]上单调递减,在[ ,2]上单调递增,
,2]上单调递增,f(
 )=3,f,2)=
)=3,f,2)= ,因此最大值为x=2时,y=
,因此最大值为x=2时,y= ,最小值为x=
,最小值为x= 时,y=2
时,y=2
综上所述,
 的最大值为
的最大值为 ,,最小值为2
,,最小值为2
分析:(1)令x=0,y=2,代入可得答案;
(2)设
 ,
, ,作差后由函数的性质可判单调性;
,作差后由函数的性质可判单调性;(3)由(2)及已知条件化简所给函数,由函数的单调性可得最值.
点评:本题为抽象函数的综合应用,涉及函数的单调性和最值,属中档题.

练习册系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |