题目内容
已知圆 ,直线
,直线 。
。
(Ⅰ)求证:对 ,直线
,直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)设 与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程;
(Ⅲ)若定点P(1,1)分弦AB为 ,求此时直线
,求此时直线 的方程
的方程
【答案】
(Ⅰ)解法一:圆 的圆心为
的圆心为 ,半径为
,半径为 。
。
∴圆心C到直线 的距离
的距离
∴直线 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;

方法二:∵直线 过定点
过定点 ,而点
,而点 在圆
在圆 内∴直线
内∴直线 与圆C相交,即直线
与圆C相交,即直线 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)当M与P不重合时,连结CM、CP,则 ,
,
∴
设 ,则
,则 ,
,
化简得:
当M与P重合时, 也满足上式。
也满足上式。
故弦AB中点的轨迹方程是 。
。
(Ⅲ)设 ,由
,由 得
得 ,
,
∴ ,化简的
,化简的 ………………①
………………①
又由 消去
消去 得
得 ……………(*)
……………(*)
∴ ………………………………②
………………………………②
由①②解得 ,带入(*)式解得
,带入(*)式解得 ,
,
∴直线 的方程为
的方程为 或
或
【解析】略

练习册系列答案
相关题目
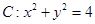 ,直线
,直线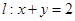 ,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.
,以O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系.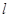 方程化为极坐标方程;
方程化为极坐标方程;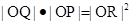 ,当点P在
,当点P在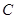 与直线
与直线 及
及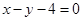 都相切,圆心在直线
都相切,圆心在直线 上,则圆
上,则圆 B、
B、
 D、
D、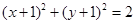
 和直线
和直线 . 若圆
. 若圆 与直线
与直线 没有公共点,则
没有公共点,则 的取值范围是
的取值范围是
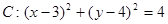 和直线
和直线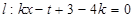 ,
,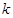 取什么值,直线和圆总相交;
取什么值,直线和圆总相交;