题目内容

如果函数f（x）=|lg|x-1||在其定义域的某个子集（k-1，k+1）上不存在反函数，那么实数k的取值范围是
-1＜k＜0或2＜k＜3
-1＜k＜0或2＜k＜3
．
分析：欲使函数f（x）在其定义域的某个子集（k-1，k+1）上不存在反函数，只需找到在某一个区间长度为2，且满足不单调的区间，画出函数的图象，结合函数图象建立关系式，解之即可．
解答：解：只要找到在某一个区间长度为2，且满足不单调的区间，那么在这个区间上就不存在反函数；
定义域为{x|x∈R且x≠1}，画出函数图象

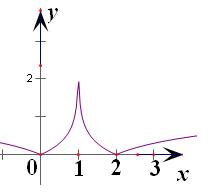
也就是说这个子区间的左端点在0到或者右端点在1到2，
∴0＜k+1＜1和1＜k-1＜2 即-1＜k＜0或2＜k＜3
故答案为：-1＜k＜0或2＜k＜3．
点评：本题主要考查了反函数的知识点，以及函数的单调性，同时考查了数形结合法，属于中档题．
练习册系列答案
相关题目
在平面直角坐标系中，横坐标、纵坐标均为整数的点称为整点，如果函数f（x）的图象恰好通过n（n∈N*）个整点，则称函数f（x）为n阶整点函数、有下列函数：①f（x）=sin 2x；②g（x）=x3；③h（x）=（(
13
)）x；④φ（x）=ln x，其中是一阶整点函数的是
 
．
如果函数f（x）=x2+2（a-1）x+2在区间（-∞，4]上是减少的，那么实数a的取值范围是（　　）
（2012•安徽模拟）如果函数f（x）=cos（2x+φ）的图象关于点(
4π
3
，0)成中心对称，且-
π
2
＜φ＜
π
2
，则函数y=f(x+
π
3
)为（　　）
如果函数f（x）满足：对任意实数a，b都有f（a+b）=f（a）f（b），且f（1）=2，则
f(2)
f(1)
+
f(3)
f(2)
+
f(4)
f(3)
+
f(5)
f(4)
+…+
f(2010)
f(2009)
=
4018
4018
．
如果函数f（x）在区间D上是凸函数，那么对于区间D内的任意x1，x2，…，xn，都有
f(x1)+f(x2)+…+f(xn)
n
≤f（
x1+x2+…+xn
n
）．若y=sinx在区间（0，π）上是凸函数，那么在△ABC中，sinA+sinB+sinC的最大值是
3
3
2
3
3
2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网