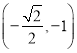题目内容
【题目】已知函数
，则函数
的图象为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】
写出分段函数，分段求导后利用导函数的符号或导函数的零点判断函数f（x）的图象的形状．
=
，
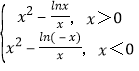当x＜0时，
=
．
令g（x）=2x3﹣1+ln（﹣x），
由
，得
，
当x∈（﹣∞，
）时，g′（x）＞0，当x∈（，0）时，g′（x）＜0．
所以g（x）有极大值为
=
．
又x2＞0，所以f′（x）的极大值小于0．
所以函数f（x）在（﹣∞，0）上为减函数．
当x＞0时，
=
．
令h（x）=2x3﹣1+lnx，
．
所以h（x）在（0，+∞）上为增函数，而h（1）=1＞0，h（
）=﹣
．
又x2＞0，所以函数f′（x）在（0，+∞）上有一个零点，则原函数有一个极值点．
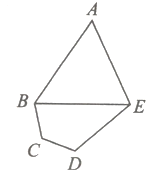
综上函数f（x）的图象为D中的形状．
故选：D．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某大型水果超市每天以
元/千克的价格从水果基地购进若干
水果，然后以
元/千克的价格出售，若有剩余，则将剩下的水果以
元/千克的价格退回水果基地，为了确定进货数量，该超市记录了水果最近
天的日需求量（单位：千克），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以天记录的各日需求量的频率代替各日需求量的概率.
（1）求该超市水果日需求量
（单位：千克）的分布列；
（2）若该超市一天购进水果
千克，记超市当天水果获得的利润为
（单位：元），求的分布列及其数学期望.
