题目内容
9. 如图,已知扇形OAB和OA1B1,A1为OA的中点,若扇形OA1B1的面积为1,则扇形OAB的面积为4.
如图,已知扇形OAB和OA1B1,A1为OA的中点,若扇形OA1B1的面积为1,则扇形OAB的面积为4.
分析 设∠AOB=α,在扇形OA1B1中,利用扇形的面积公式可求OA12α=2,根据已知OA=2OA1,在扇形OAB中,利用扇形的面积公式即可计算得解.
解答 解:设∠AOB=α,
∵扇形OA1B1的面积为1,即:1=$\frac{1}{2}$OA12α,
∴解得:OA12α=2,
∵A1为OA的中点,OA=2OA1,
∴在扇形OAB中,S扇形OAB=$\frac{1}{2}$OA2α=$\frac{1}{2}×$(2OA1)2α=2OA12α=2×2=4.
故答案为:4.
点评 本题主要考查了扇形的面积公式的应用,考查了数形结合思想和转化思想,属于基础题.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
4.已知定义在R上的函数f(x),周期为4,当x∈[0,4)时,f(x)=$\left\{\begin{array}{l}{-{x}^{2}+2x,0≤x<2}\\{2x-4,2≤x<4}\end{array}\right.$,当x∈(-4,b)时,函数y=f(x)-1有5个零点,则实数b的取值范围为( )
| A. | (5,$\frac{13}{2}$] | B. | [5,$\frac{13}{2}$) | C. | (5,$\frac{13}{2}$) | D. | [5,$\frac{13}{2}$] |
2. 为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
 为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )
为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将数据分成[0,0.5),[0.5,1),…,[4,4.5)9组,绘制成了如图所示的频率分布直方图.由图可知,居民月均用水量的众数、中位数的估计值分别为( )| A. | 2.25,2.25 | B. | 2.25,2.02 | C. | 2,2.5 | D. | 2.5,2.25 |
14.执行图示的程序框图,则输出的结果为( )
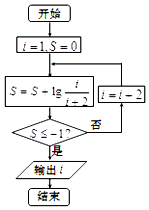

| A. | 7 | B. | 9 | C. | 10 | D. | 11 |
1. 我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
 我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )
我国南宋数学家秦九韶(约公园1202-1261年)给出了求n(n∈N*)次多项式anxn+an-1xn-1+…+a1x+a0的值的一种简捷算法,改算法被后人命名为“秦九韶算法”,其程序框图如图所示.当x=0.4时,多项式x4+0.6x3+x2-2.56x+1的值为( )| A. | 0.2 | B. | 1.58944 | C. | 1.26176 | D. | 2.248 |
2.已知集合A={1,2,3},B={x|x2-4<0},则A∩B=( )
| A. | {1} | B. | {1,2} | C. | {2} | D. | {2,3} |