题目内容
设函数 ,记
,记 的导函数
的导函数 ,
, 的导函数
的导函数 ,
,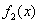 的导函数
的导函数 ,…,
,…, 的导函数
的导函数 ,
, .
.
(1)求 ;
;
(2)用n表示 ;
;
(3)设 ,是否存在
,是否存在 使
使 最大?证明你的结论.
最大?证明你的结论.
(1) (2)
(2) (3)故当
(3)故当 或
或 时,
时, 取
取
最大值 .
.
解析试题分析:⑴易得, ,
, 
 ,所以
,所以
⑵不失一般性,设函数 的导函数为
的导函数为 ,其中
,其中 ,常数
,常数 ,
, .
.
对 求导得:
求导得:
故由 得:
得: ①,
①, ②,
②,  ③
③
由①得: ,
,
代入②得: ,即
,即 ,其中
,其中
故得: .
.
代入③得: ,即
,即 ,其中
,其中 .
.
故得: ,
,
因此
 .
.
将 代入得:
代入得: ,其中
,其中 .
.
(3)由(1)知 ,
,
当 时,
时, ,
, ,故当
,故当 最大时,
最大时, 为奇数.
为奇数.
当 时,
时,
又 ,
,

 ,
, ,因此数列
,因此数列 是递减数列
是递减数列
又 ,
, ,
,
故当 或
或 时,
时, 取最大值
取最大值 .
.
考点:导数 数列综合
点评:本题是数列综合题,利用转化法把非常规数列转化成等差或等比数列来处理是关键,
属难题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 ,请用定义证明
,请用定义证明 在
在
 上为减函数.
上为减函数. 对定义域内任意
对定义域内任意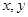 ,有
,有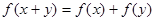
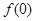 ;
;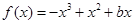 ,
,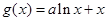 (
(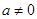 )
) 存在极值点,求实数b的取值范围;
存在极值点,求实数b的取值范围;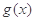 的单调区间;
的单调区间;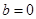 且
且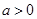 时,令
时,令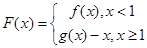 ,
,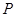 (
(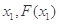 ),
),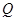 (
(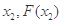 )为曲线y=
)为曲线y=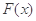 上的两动点,O为坐标原点,能否使得
上的两动点,O为坐标原点,能否使得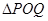 是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由。
是以O为直角顶点的直角三角形,且斜边中点在y轴上?请说明理由。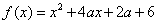 .
. 的值域为
的值域为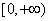 ,求
,求 的值;
的值;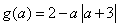 的值域.
的值域.
 时,求
时,求 在[1,
在[1, ]上的取值范围。
]上的取值范围。 在[1,
在[1,
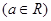 .
.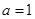 时,证明:
时,证明: 在
在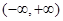 上为减函数;
上为减函数;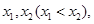 求实数
求实数 的取值范围.
的取值范围.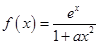 ,其中
,其中 为正实数.
为正实数.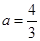 时,求
时,求 的极值点;
的极值点;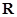 上的单调函数,求
上的单调函数,求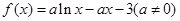 .
.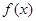 的单调区间
的单调区间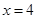 处切线的斜率为
处切线的斜率为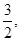 若函数
若函数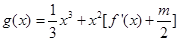 在区间(1,3)上不是单调函数,求m的取值范围
在区间(1,3)上不是单调函数,求m的取值范围