题目内容
已知（a2+1）n展开式中的各项系数之和等于（
x2+
）5的展开式的常数项，而（a2+1）n的展开式的系数最大的项等于54，求a的值（a∈R）.
x2+）5的展开式的常数项，而（a2+1）n的展开式的系数最大的项等于54，求a的值（a∈R）.a=±
（x2+）5的通项公式为
Tr+1=C
·
=C·
·x
令20-5r=0，则r=4，∴常数项为T5=C
×=16.
又（a2+1）n展开式的各项系数之和为2n，依题意得2n=16，
n=4，由二项式系数的性质知（a2+1）4展开式中系数最大的项是中间项T3，所以C
（a2）2=54，即a4=9，所以a=±.
x2+）5的通项公式为Tr+1=C
·=C··x令20-5r=0，则r=4，∴常数项为T5=C
×=16.又（a2+1）n展开式的各项系数之和为2n，依题意得2n=16，
n=4，由二项式系数的性质知（a2+1）4展开式中系数最大的项是中间项T3，所以C
（a2）2=54，即a4=9，所以a=±.
练习册系列答案
相关题目
+
)n (n∈N*)的展开式中第5项的系数与第3项的系数之比为10∶1.求展开式中系数最大的是第几项？
展开式的第4项含x3，则n的值为___________．
按
的降幂排列展开，若
，
，且
，当展开式第二项与第三项值相等时，
的展开式中，含
的项的二项式系数是以an=2n+1为通项的数列{an}的（ ）
．第37项 C．第38项 D．第39项
)6展开式中常数项为（ ）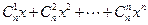
能被
整除，则
的值可能为 （ ）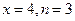
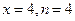
第2个数是_________.
则
的值为_