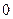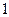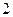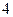题目内容
(本小题满分12 分)
已知函数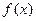 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的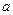 、
、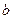 ∈R,都满足
∈R,都满足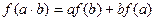 ,若
,若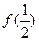 =1,
=1,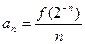 ;
;
(1)求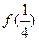 、
、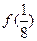 、
、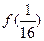 的值;
的值;
(2)猜测数列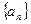 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。
已知函数
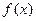 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的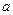 、
、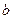 ∈R,都满足
∈R,都满足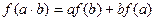 ,若
,若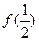 =1,
=1,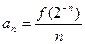 ;
;(1)求
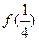 、
、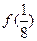 、
、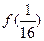 的值;
的值;(2)猜测数列
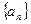 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。(1) ;
; ;
; 。
。
(2)
 ;
; ;
; 。
。(2)

(1)

 -----------------------------3分
-----------------------------3分
(2)由(1)可猜测: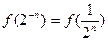 =n´
=n´ ---------------------------------------5分
---------------------------------------5分
下用数学归纳法证明:
当n=1时,左边= 右式= 1´
右式= 1´ \ n=1时,命题成立。
\ n=1时,命题成立。
假设n=k时,命题成立,即: =k´
=k´ ,------------------------------7分
,------------------------------7分
则n=k+1时,左边=
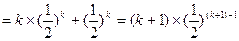 -----------------10分
-----------------10分
\ n=k+1时,命题成立。
综上可知:对任意n∈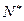 都有
都有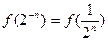 =n´
=n´ 。----------------------------11分
。----------------------------11分
所以: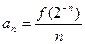 =
=  。-----------------------------------------------------------------12分
。-----------------------------------------------------------------12分


 -----------------------------3分
-----------------------------3分(2)由(1)可猜测:
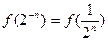 =n´
=n´ ---------------------------------------5分
---------------------------------------5分下用数学归纳法证明:
当n=1时,左边=
 右式= 1´
右式= 1´ \ n=1时,命题成立。
\ n=1时,命题成立。假设n=k时,命题成立,即:
 =k´
=k´ ,------------------------------7分
,------------------------------7分则n=k+1时,左边=

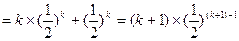 -----------------10分
-----------------10分\ n=k+1时,命题成立。
综上可知:对任意n∈
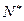 都有
都有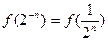 =n´
=n´ 。----------------------------11分
。----------------------------11分所以:
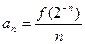 =
=  。-----------------------------------------------------------------12分
。-----------------------------------------------------------------12分
练习册系列答案
相关题目
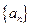 中,
中, ,
,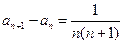 (
(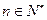 )
)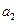 、
、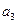 的值;
的值;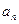 ;
;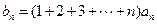 ,求
,求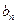 的最小值.
的最小值.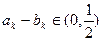 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.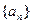 中,若
中,若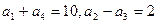 ,则此数列的前
,则此数列的前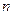 项和
项和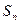 是( )
是( )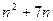
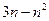
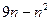
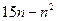
 满足
满足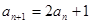 ,
,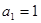 ,则
,则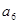 =( )
=( ) 中,若三个内角
中,若三个内角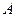 、
、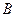 、
、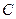 成等差数列,且
成等差数列,且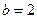 ,则
,则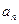 = .
= .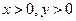 ,若
,若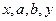 成等差数列,
成等差数列,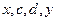 成等比数列,则
成等比数列,则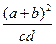 的最小值为
的最小值为