题目内容
抛掷两枚骰子,设出现的点数之和是6,7,8的概率依次是P(A),P(B),P(C),则
- A.P(A)=P(C)<P(B)
- B.P(A)<P(B)<P(C)
- C.P(B)<P(A)=P(C)
- D.P(C)<P(B)<P(A)
A
分析:我们列出先后抛掷两枚骰子出现的点数的所有的基本事件个数,再分别求出点数之和是6,7,8的基本事件个数,进而求出点数之和是6,7,8的概率P(A),P(B),P(C),即可得到它们的大小关系.
解答:先后抛掷两枚骰子,出现的点数共有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种
其中点数之和是6的有5种,故P(A)= ;
;
点数之和是7的有6种,P(B)=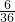
点数之和是8的有5种,故P(C)= .
.
∴P(A)=P(C)<P(B).
故选A.
点评:本题考查的知识点是古典概型及其概率计算公式,其中根据已知利用古典概型概率公式,分别计算出出现的点数之和是6,7,8的概率依次是P(A),P(B),P(C),是解答本题的关键.
分析:我们列出先后抛掷两枚骰子出现的点数的所有的基本事件个数,再分别求出点数之和是6,7,8的基本事件个数,进而求出点数之和是6,7,8的概率P(A),P(B),P(C),即可得到它们的大小关系.
解答:先后抛掷两枚骰子,出现的点数共有:
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种
其中点数之和是6的有5种,故P(A)=
 ;
;点数之和是7的有6种,P(B)=
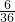
点数之和是8的有5种,故P(C)=
 .
.∴P(A)=P(C)<P(B).
故选A.
点评:本题考查的知识点是古典概型及其概率计算公式,其中根据已知利用古典概型概率公式,分别计算出出现的点数之和是6,7,8的概率依次是P(A),P(B),P(C),是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
先后抛掷两枚骰子,设出现的点数之和是12、11、10的概率依次是P1、P2、P3,则( )
| A、P1=P2<P3 | B、P1<P2<P3 | C、P1<P2=P3 | D、P3=P2<P1 |