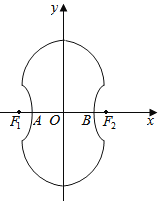题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.设不经过焦点
的左、右焦点.设不经过焦点![]() 的直线
的直线![]() 与椭圆交于两个不同的点
与椭圆交于两个不同的点![]() 、
、![]() ,焦点
,焦点![]() 到直线
到直线![]() 的距离为
的距离为![]() .若直线
.若直线![]() 、
、![]() 、
、![]() 的斜率依次成等差数列,求
的斜率依次成等差数列,求![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】
设直线![]() ,点
,点![]() ,
,![]() ,联立直线和椭圆的方程,得到韦达定理,根据直线
,联立直线和椭圆的方程,得到韦达定理,根据直线![]() 、
、![]() 、
、![]() 的斜率依次成等差数列得到
的斜率依次成等差数列得到![]() ,代入
,代入![]() 得
得![]() ,
,
求出d=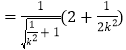 ,再求函数d(k)的取值范围得解.
,再求函数d(k)的取值范围得解.
由条件,知点![]() 、
、![]() .
.
设直线![]() ,点
,点![]() ,
,![]() .
.
则![]() 、
、![]() 满足
满足![]() ,即
,即
![]() . ①
. ①
由于点![]() 与
与![]() 不重合,且直线
不重合,且直线![]() 的斜率存在,故
的斜率存在,故![]() 、
、![]() 为方程①的两个不同实根.
为方程①的两个不同实根.
因此,式①的判别式
![]()
![]()
![]() . ②
. ②
由直线![]() 、
、![]() 、
、![]() 的斜率
的斜率![]() 、
、![]() 、
、![]() 依次成等差数列,知
依次成等差数列,知
![]()
![]()
![]() .
.
假设![]() .则直线
.则直线![]() 的方程为
的方程为![]() ,即
,即![]() 经过点
经过点![]() ,不符合条件.
,不符合条件.
因此,![]() .
.
故由方程①及韦达定理知
![]()
![]() . ③
. ③
由式②、③知
![]()
![]() .
.
反之,当![]() 、
、![]() 满足式③及
满足式③及![]() 时,直线
时,直线![]() 必不过点
必不过点![]() (否则,将导致
(否则,将导致![]() ,与式③矛盾).
,与式③矛盾).
而此时![]() 、
、![]() 满足式②,故直线
满足式②,故直线![]() 与椭圆有两个不同的交点
与椭圆有两个不同的交点![]() 、
、![]() ,同时,也保证了
,同时,也保证了![]() 、
、![]() 的斜率存在(否则,
的斜率存在(否则,![]() 、
、![]() 中的某一个为
中的某一个为![]() ,结合
,结合![]() ,知
,知![]() ,与方程①有两个不同的实根矛盾).
,与方程①有两个不同的实根矛盾).
又点![]() 到
到![]() 的距离为
的距离为
![]()
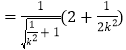 . ④
. ④
注意到,![]() .
.
令![]() .则
.则![]() .
.
故式④可改写为
![]() . ⑤
. ⑤
考虑到函数![]() 在区间
在区间![]() 上单调递减,故由式⑤得
上单调递减,故由式⑤得
![]() .
.

练习册系列答案
相关题目