题目内容
已知向量m=(-1,cosωx+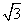 sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为
sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为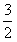 π,
π,
(Ⅰ)求ω的值;
(Ⅱ)设α是第一象限角,且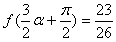 ,求
,求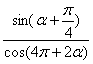 的值。
的值。
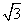 sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为
sinωx),n=(f(x),cosωx),其中ω>0,且m⊥n,又函数f(x)的图象任意两相邻对称轴间距为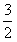 π,
π,(Ⅰ)求ω的值;
(Ⅱ)设α是第一象限角,且
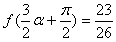 ,求
,求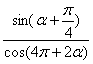 的值。
的值。解:(Ⅰ)由题意,得m·n=0,
所以
 ,
,
根据题意知,函数f(x)的最小正周期为3π,
又ω>0,
所以 ;
;
(Ⅱ)由(Ⅰ)知 ,
,
所以 ,
,
解得 ,
,
因为α是第一象限角,故 ,
,
所以, 。
。
所以

 ,
,根据题意知,函数f(x)的最小正周期为3π,
又ω>0,
所以
 ;
;(Ⅱ)由(Ⅰ)知
 ,
,所以
 ,
,解得
 ,
,因为α是第一象限角,故
 ,
,所以,
 。
。
练习册系列答案
相关题目
已知向量
=(-x+1,2),
=(3,2y-1),若
⊥
,则8x+(
)y的最小值为( )
| m |
| n |
| m |
| n |
| 1 |
| 16 |
| A、2 | ||
| B、4 | ||
C、2
| ||
D、4
|