题目内容
16.设函数f(x)=|ex-e2a|,若f(x)在区间(-1,3-a)内的图象上存在两点,在这两点处的切线互相垂直,则实数a的取值范围是(-$\frac{1}{2}$,$\frac{1}{2}$).分析 求出函数f(x)的表达式,利用数形结合,结合导数的几何意义进行求解即可.
解答 解:当x≥2a时,f(x)=|ex-e2a|=ex-e2a,此时为增函数,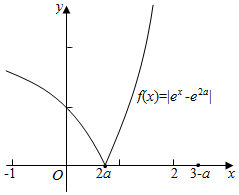
当x<2a时,f(x)=|ex-e2a|=-ex+e2a,此时为减函数,
即当x=2a时,函数取得最小值0,
设两个切点为M(x1,f(x1)),N((x2,f(x2)),
由图象知,当两个切线垂直时,必有,x1<2a<x2,
即-1<2a<3-a,得-$\frac{1}{2}$<a<1,
∵k1k2=f′(x1)f′(x2)=ex1•(-ex2)=-ex1+x2=-1,
则ex1+x2=1,即x1+x2=0,
∵-1<x1<0,∴0<x2<1,且x2>2a,
∴2a<1,解得a<$\frac{1}{2}$,
综上-$\frac{1}{2}$<a<$\frac{1}{2}$,
故答案为:(-$\frac{1}{2}$,$\frac{1}{2}$).
点评 本题主要考查导数的几何意义的应用,利用数形结合以及直线垂直的性质是解决本题的关键,属于中档题..

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
8.设m,n为两条不同的直线,α,β,γ为三个不同的平面,则下列四个命题中为真命题的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m∥α,m∥β,则α∥β | ||
| C. | 若m∥α,n∥β,m∥n,则α∥β | D. | 若α∥β,α∩γ=m,β∩γ=n,则m∥n |
5.已知点F1,F2是椭圆C:$\frac{x^2}{4}+{y^2}$=1的焦点,点M在椭圆C上且满足|$\overrightarrow{M{F}_{1}}$+$\overrightarrow{M{F}_{2}}$|=2$\sqrt{3}$,则△MF1F2的面积为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | 2 |
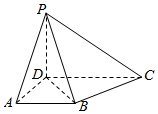 在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.
在四棱锥P-ABCD中,AD⊥平面PDC,PD⊥DC,底面ABCD是梯形,AB∥DC,AB=AD=PD=1,CD=2.