题目内容
自选题：已知函数f（x）=|x﹣8|﹣|x﹣4|．
（Ⅰ）作出函数y=f（x）的图象；
（Ⅱ）解不等式|x﹣8|﹣|x﹣4|＞2．
（Ⅰ）作出函数y=f（x）的图象；
（Ⅱ）解不等式|x﹣8|﹣|x﹣4|＞2．
解： （Ⅰ）f（x）=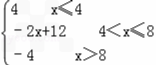
图象如下：
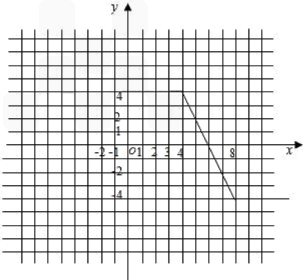
（Ⅱ） 不等式|x﹣8|﹣|x﹣4|＞2，即f（x）＞2，观察知当4＜x＜8时，存在函数值为2的点． 由﹣2x+12=2得x=5．
由函数f（x）图象可知，原不等式的解集为（﹣∞，5）．
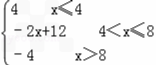图象如下：（Ⅱ） 不等式|x﹣8|﹣|x﹣4|＞2，即f（x）＞2，观察知当4＜x＜8时，存在函数值为2的点． 由﹣2x+12=2得x=5．
由函数f（x）图象可知，原不等式的解集为（﹣∞，5）．
练习册系列答案
相关题目
自选题：已知函数f（x）=|x-8|-|x-4|．
