题目内容
抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值是
【答案】分析:先对y=-x2求导得到与直线4x+3y-8=0平行的切线的切点坐标,再由点到线的距离公式可得答案.
解答:解:先对y=-x2求导得y′=-2x
令y′=-2x=-
易得x=
即切点P( ,-
,- )
)
利用点到直线的距离公式得
d=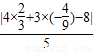 =
=
故答案为:
点评:本题主要考查抛物线的基本性质和点到线的距离公式.考查综合运用能力.
解答:解:先对y=-x2求导得y′=-2x
令y′=-2x=-

易得x=

即切点P(
 ,-
,- )
)利用点到直线的距离公式得
d=
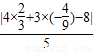 =
=
故答案为:

点评:本题主要考查抛物线的基本性质和点到线的距离公式.考查综合运用能力.

练习册系列答案
相关题目
抛物线y=x2上的点到直线4x-3y-8=0的距离的最小值是( )
A、
| ||
B、
| ||
C、
| ||
| D、3 |