题目内容
已知函数 (
( ),其图像在点(1,
),其图像在点(1, )处的切线方程为
)处的切线方程为 .
.
(1)求 ,
, 的值;
的值;
(2)求函数 的单调区间和极值;
的单调区间和极值;
(3)求函数 在区间[-2,5]上的最大值.
在区间[-2,5]上的最大值.
【答案】
(1) 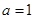 ,
,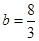 .
.
(2)函数 的极大值是
的极大值是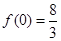 ,极小值是
,极小值是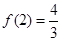 .
.
(3)函数 在区间
在区间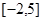 上的最大值为
上的最大值为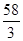 .
.
【解析】
试题分析:(1) 由题意,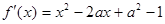 .
1分
.
1分
又∵函数 的图象在点
的图象在点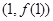 处的切线方程为
处的切线方程为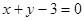 ,
,
所以切线的斜率为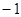 ,
,
即 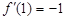 ,∴
,∴ ,解得
,解得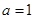 .
2分
.
2分
又∵点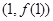 在直线
在直线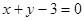 上,∴
上,∴ , 3分
, 3分
同时点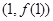 即点
即点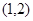 在
在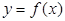 上,
上,
∴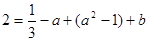 , 4分
, 4分
即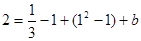 ,解得
,解得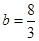 . 5分
. 5分
(2)由(1)有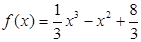 ,
,
∴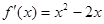 ,
6分
,
6分
由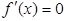 可知
可知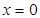 ,或
,或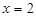 ,所以有
,所以有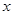 、
、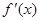 、
、 的变化情况表如下:
的变化情况表如下:
|
|
|
|
|
|
|
|
|
+ |
|
- |
|
+ |
|
|
|
极大值 |
|
极小值 |
|
8分
由上表可知, 的单调递增区间是
的单调递增区间是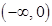 和
和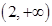 ,单调递减区间是
,单调递减区间是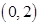 ; 10分
; 10分
∴函数 的极大值是
的极大值是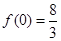 ,极小值是
,极小值是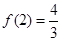 .
11分
.
11分
(3)由(2),函数 在区间
在区间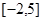 上的极大值是
上的极大值是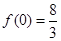 .
12分
.
12分
又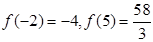 ,
13分
,
13分
∴函数 在区间
在区间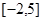 上的最大值为
上的最大值为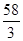 . 14分
. 14分
考点:导数的几何意义,应用导数研究函数的单调性、极(最值)值。
点评:典型题,本题属于导数内容中的基本问题,(1)运用“函数在某点的切线斜率,就是该点的导数值”,确定直线的斜率。通过研究导数值的正负情况,明确函数的单调区间。确定函数的最值,往往遵循“求导数,求驻点,计算极值、端点函数值,比较大小确定最值”。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
已知函数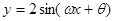 为偶函数
为偶函数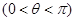 ,其图像与直线
,其图像与直线 的某两个交点的横坐标为
的某两个交点的横坐标为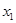 ,
,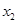 ,若
,若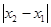 的最小值为
的最小值为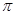 ,则( )
,则( )
A.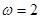 , ,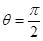 | B.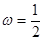 , ,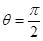 |
C.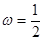 , ,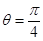 | D.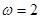 , ,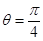 |




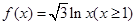 ,若将其图像绕原点逆时针旋转
,若将其图像绕原点逆时针旋转 角后,所得图像仍是某函数的图像,则当角
角后,所得图像仍是某函数的图像,则当角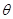 取最大值
取最大值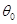 时,
时,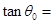 ( )
( ) B.
B.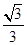 C.
C.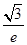 D.
D.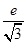
 是偶函数,其图像与x轴有四个交点,则方程
是偶函数,其图像与x轴有四个交点,则方程 的所有实数根的和为( )
的所有实数根的和为( ) 为偶函数
为偶函数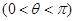 ,其图像与直线
,其图像与直线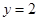 的某两个交点的横坐标为
的某两个交点的横坐标为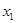 ,
,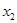 ,若
,若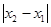 的最小值为
的最小值为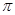 ,则( )
,则( )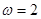 ,
,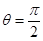 B.
B.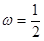 ,
,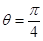 D.
D.