题目内容
给出下列三个类比结论：
①(ab)n＝anbn与(a＋b)n类比，则有(a＋b)n＝an＋bn；
②loga(xy)＝logax＋logay与sin(α＋β)类比，则有sin(α＋β)＝sin αsin β；
③(a＋b)2＝a2＋2ab＋b2与(a＋b)2类比，则有(a＋b)2＝a2＋2a·b＋b2.
其中结论正确的个数是( )．
A．0 B．1 C．2 D．3
解 (1)对∀x∈R有－x∈R，并且f(－x)＝
＝
＝－＝－f(x)，所以f(x)是奇函数．
(2)法一 f(x)在R上单调递增，证明如下：
任取x1，x2∈R，并且x1＞x2，
f(x1)－f(x2)＝
－
＝
＝
.
∵x1＞x2，∴2x1＞2x2＞0，
即2x1－2x2＞0，又∵2x1＋1＞0,2x2＋1＞0.
∴＞0.
∴f(x1)＞f(x2)．
∴f(x)在R上为单调递增函数．
法二 f′(x)＝
＞0
∴f(x)在R上为单调递增函数．
练习册系列答案
阅读快车系列答案
相关题目
；
；
；
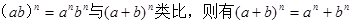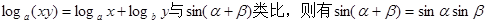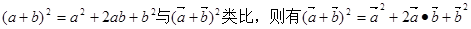