题目内容
已知函数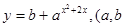 是常数
是常数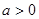 且
且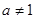 )在区间
)在区间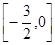 上有
上有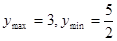
(1)求 的值;
的值;
(2)若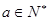 当
当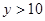 时,求
时,求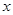 的取值范围;
的取值范围;
⑴ 或
或 ;⑵
;⑵ 或
或 .
.
解析试题分析:⑴先求出指数 的取值区间,然后根据指数函数的性质对
的取值区间,然后根据指数函数的性质对 进行讨论,根据指数函数的性质判断函数的单调性,与最值结合即能解出参数的值;⑵根据参数的取值集合先确定参数的具体值,代入不等式根据指数函数的单调性解不等式即可.
进行讨论,根据指数函数的性质判断函数的单调性,与最值结合即能解出参数的值;⑵根据参数的取值集合先确定参数的具体值,代入不等式根据指数函数的单调性解不等式即可.
试题解析:(1)因为 ,∴
,∴ 值域为
值域为 ,即
,即 , 2分
, 2分
若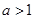 ,函数
,函数 在
在 上单调递增,
上单调递增,
所以, 则
则 ,
,
 , .4分
, .4分
若 ,函数
,函数 在
在 上单调递减,
上单调递减,
所以 则
则 ,
, , .6分
, .6分
所求 ,
, 的值为
的值为 或
或 ; 7分
; 7分
(2)由(1)可知 ,
, , ..8分
, ..8分
则 ,得
,得 即
即 ,
,
解得 或
或 . .12分
. .12分
考点:指数型复合函数的性质及应用,不等式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 辟为水果园,其中
辟为水果园,其中 ,
, 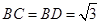 ,
, .若经过
.若经过 上一点
上一点 和
和 上一点
上一点 铺设一条道路
铺设一条道路 ,且
,且 .
.
 的关系式;
的关系式; 的位置在哪里?
的位置在哪里? (升)关于行驶速度
(升)关于行驶速度 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.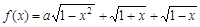 的最大值为
的最大值为 .
.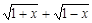 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;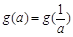 的所有实数a.
的所有实数a.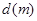 与车速
与车速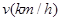 和车长
和车长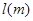 的关系满足:
的关系满足: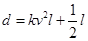 (
( 为正的常数),假定车身长为
为正的常数),假定车身长为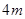 ,当车速为
,当车速为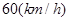 时,车距为2.66个车身长.
时,车距为2.66个车身长.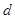 关于车速
关于车速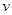 的函数关系式;
的函数关系式;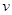 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度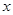 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当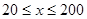 时,车流速度
时,车流速度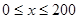 时,求函数
时,求函数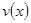 的表达式;
的表达式;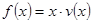 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).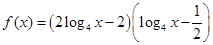 。
。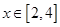 时,求该函数的值域;
时,求该函数的值域; 对于
对于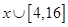 恒成立,求
恒成立,求 有取值范围。
有取值范围。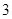 年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第
年内(按36个月计)全部还清.签约的单位提供的工资标准为第一年内每月1500元,第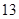 个月开始,每月工资比前一个月增加
个月开始,每月工资比前一个月增加 直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多
直到4000元.小王计划前12个月每个月还款额为500,第13个月开始,每月还款额比前一个月多 元.
元. 个月还清贷款(
个月还清贷款( ),试用
),试用 表示小王第
表示小王第 )个月的还款额
)个月的还款额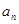 ;
; 时,小王将在第几个月还清最后一笔贷款?
时,小王将在第几个月还清最后一笔贷款? 元的基本生活费?(参考数据:
元的基本生活费?(参考数据: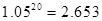 )
)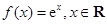 .
. 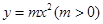 公共点的个数.
公共点的个数. 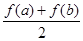 与
与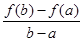 的大小, 并说明理由.
的大小, 并说明理由.