题目内容
设a为实数,记函数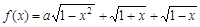 的最大值为
的最大值为 .
.
(1)设t=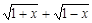 ,求t的取值范围,并把f(x)表示为t的函数m(t) ;
,求t的取值范围,并把f(x)表示为t的函数m(t) ;
(2)求 ;
;
(3)试求满足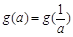 的所有实数a.
的所有实数a.
(1)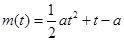 ,
, ;(2)
;(2) =
=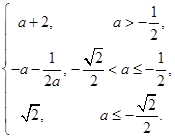 (3)
(3) .
.
解析试题分析:(1)根据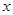 的取值范围求出
的取值范围求出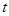 的范围,再将
的范围,再将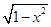 用含
用含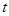 的式子表示;(2)由题意知
的式子表示;(2)由题意知 即为函数
即为函数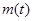
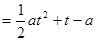 ,
,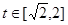 的最大值,因为对称轴含有参数
的最大值,因为对称轴含有参数 ,所以要讨论处理;(3)根据(2)问得出的
,所以要讨论处理;(3)根据(2)问得出的 ,由
,由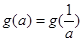 在对应区域上讨论解答即可.
在对应区域上讨论解答即可.
试题解析:(1)∵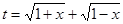 ,∴要使
,∴要使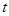 有意义,必须
有意义,必须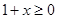 且
且 ,即
,即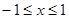 .
.
∵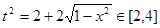 ,且
,且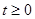 ①
①
∴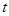 的取值范围是
的取值范围是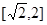 , 2分
, 2分
由①得: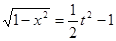 ,
,
∴
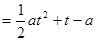 ,
,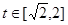 . 4分
. 4分
(2)由题意知 即为函数
即为函数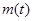
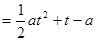 ,
,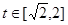 的最大值,
的最大值,
∵直线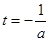 是抛物线
是抛物线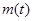
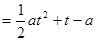 的对称轴, 5分
的对称轴, 5分
∴可分以下几种情况进行讨论:
①当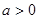 时,函数
时,函数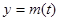 ,
,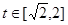 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由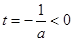 知
知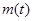 在
在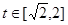 上单调递增,故
上单调递增,故

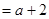 ;
;
②当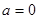 时,
时,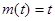 ,
,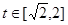 ,有
,有 =2;
=2;
③当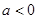 时,,函数
时,,函数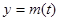 ,
,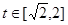 的图象是开口向下的抛物线的一段,
的图象是开口向下的抛物线的一段,
若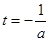
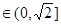 即
即 时,
时,
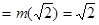 ,
,
若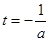
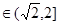 即
即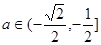 时,
时,
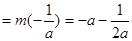 ,
,
若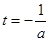
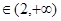 即
即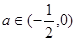 时,
时,

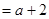 . 9分
. 9分
综上所述,有 =
=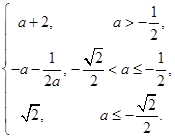 10分
10分
(3)当 时,
时,
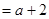
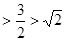 ;
;
当

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 上的函数
上的函数
 ,当
,当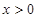 时,
时,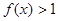 ,且对任意的
,且对任意的 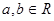 ,有
,有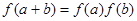 ,
,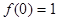 ;
;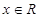 ,恒有
,恒有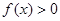 ;
;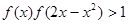 ,求
,求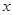 的取值范围.
的取值范围. 、圆心角为
、圆心角为 的扇形的弧上任取一点
的扇形的弧上任取一点 ,作扇形的内接矩形
,作扇形的内接矩形 ,使点
,使点 在
在 上,点
上,点 在
在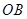 上,设矩形
上,设矩形 ,
,
 ,将
,将 的函数关系式;
的函数关系式; ,将
,将 的函数关系式;
的函数关系式;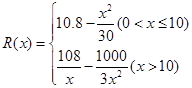
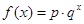 ;②
;②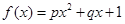 ;③
;③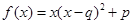 .(以上三式中
.(以上三式中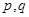 均为常数,且
均为常数,且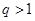 )
)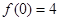 ,
,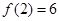 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是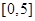 .其中
.其中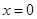 表示8月1日,
表示8月1日,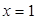 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);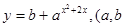 是常数
是常数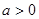 且
且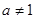 )在区间
)在区间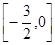 上有
上有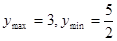
 的值;
的值; 当
当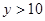 时,求
时,求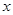 的取值范围;
的取值范围;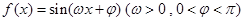 在一个周期内的部分对应值如下表:
在一个周期内的部分对应值如下表:
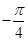

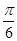

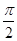
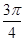


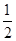
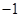
 的解析式;
的解析式;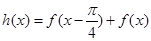 ,
,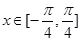 ,求
,求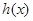 的最大值和最小值.
的最大值和最小值.  (万元)随投资收益
(万元)随投资收益 (万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%.
(万元)的增加而增加,但奖金总数不超过9万元,同时奖金不超过投资收益的20%. 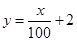 ;②
;②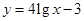 .
.