题目内容

设函数

   （1）求函数的单调区间；

   （2）求在[—1，2]上的最小值；

   （3）当时，用数学归纳法证明：

（1）函数的增区间为    （2）     （3）见解析


解析:

  （1）…………2分

令

—2

（-2，0）

0

（0，1）

1

—

0

+

0

—

0

+

减

极小

增

极大

减

极小

增

函数的增区间为

…………5分

   （2）当

所以  ………………8分

   （3）设

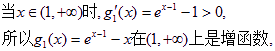
；  ………………10分

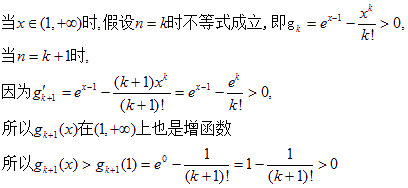
即当时，不等式成立。

所以当时，  ………………14分

练习册系列答案
相关题目
设函数f（x）=x2+bln（x+1），其中b≠0．
（1）若b=-12，求f（x）的单调递增区间；
（2）如果函f（x）在定义域内既有极大值又有极小值，求实数b的取值范围．
由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f-1（x）能确定数列bn，bn=f-1（n）若对于任意n∈N*都有bn=an，则称数列{bn}是数列{an}的“自反函数列”
（1）设函数f（x）=
px+1
x+1
，若由函数f（x）确定的数列{an}的自反数列为{bn}，求an；
（2）已知正整数列{cn}的前项和sn=
1
2
（cn+
n
cn
）．写出Sn表达式，并证明你的结论；
（3）在（1）和（2）的条件下，d1=2，当n≥2时，设dn=
-1
anSn2
，Dn是数列{dn}的前n项和，且Dn＞loga（1-2a）恒成立，求a的取值范围．
已知等差数列{an}满足：a1+a2n-1=2n，n∈N*，设Sn是数列{
1an
}的前n项和，记f（n）=S2n-Sn．
（1）求an；
（2）比较f（n+1）与f（n）的大小；
（3）（理）若不等式log2t+log2x+log2（2-x）-log2（12f（n））-3＜0对一切大于1的自然数n和所有使不等式有意义的实数x都成立，求实数t的取值范围．
（文）如果函数g（x）=x2-3x-3-12f（n）对于一切大于1的自然数n，其函数值都小于零，求x的取值范围．
设x1，x2（x1≠x2）是函数f（x）=ax3+bx2-a2x（a＞0）的两个极值点．
（1）若x1=-1，x2=2，求函f（x）的解析式；
（2）若|x1|+|x2|=2
2
，求b的最大值．
（2009•金山区一模）已知等差数列{an}满足：a1+a2n-1=2n，（n∈N*），设Sn是数列{
1an
}的前n项和，记f（n）=S2n-Sn，
（1）求an；（n∈N*）
（2）比较f（n+1）与f（n）的大小；（n∈N*）
（3）如果函数g（x）=log2x-12f（n）（其中x∈[a，b]）对于一切大于1的自然数n，其函数值都小于零，那么a、b应满足什么条件？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网