题目内容
【题目】已知函数![]() ,
,![]() ,(常数
,(常数![]() ).
).
(I)当![]() 与
与![]() 的图象相切时,求
的图象相切时,求![]() 的值;
的值;
(Ⅱ)设![]() ,讨论
,讨论![]() 在
在![]() 上零点的个数.
上零点的个数.
【答案】(I)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时,![]() 在
在![]() 上没有零点;
上没有零点;![]() 时,
时,![]() 在
在![]() 上只有一个零点;
上只有一个零点;![]() 时,
时,![]() 在
在![]() 上有两个零点.
上有两个零点.
【解析】
(I)设出切点![]() 的坐标,利用导数的几何意义求出过点A 的斜率,写出切线的点斜式方程,结合待定系数法,即可求出
的坐标,利用导数的几何意义求出过点A 的斜率,写出切线的点斜式方程,结合待定系数法,即可求出![]() 的值。
的值。
(Ⅱ)将![]() 变形得到
变形得到![]() , 当
, 当![]() 时,
时,![]() ,
,![]() 没有零点;当
没有零点;当![]() 时,
时,![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.有最小值
单调递增.有最小值![]()
![]() ,对
,对![]() 进行讨论得出
进行讨论得出![]() 在
在![]() 上零点的个数。
上零点的个数。
(I)设切点为![]() ,
,![]() ,
,
所以过![]() 点的切线方程为
点的切线方程为![]() ,即
,即![]() ,
,
所以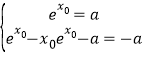 ,解得:
,解得:![]() .
.
(Ⅱ)![]() ,设函数
,设函数![]() ,
,
![]() 在
在![]() 上零点的个数与
上零点的个数与![]() 在
在![]() 上零点的个数相同,
上零点的个数相同,
当![]() 时
时![]() ,
,![]() 没有零点;
没有零点;
当![]() 时,
时,![]() ,
,
![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.
单调递增.
故![]() 是
是![]() 在
在![]() 的最小值.
的最小值.
①若![]() ,即
,即![]() ,
,![]() 在
在![]() 没有零点;
没有零点;
②若![]() ,即
,即![]() ,
,![]() 在
在![]() 只有一个零点;
只有一个零点;
③若![]() ,即
,即![]() ,由于
,由于![]() ,所以
,所以![]() 在
在![]() 上有两个零点,
上有两个零点,
综上,![]() 时,
时,![]() 在
在![]() 上没有零点;
上没有零点;![]() 时,
时,![]() 在
在![]() 上只有一个零点;
上只有一个零点;![]() 时,
时,![]() 在
在![]() 上有两个零点.
上有两个零点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目