题目内容
已知△ABC,∠C=60°,AC=2,BC=1,点M是△ABC内部或边界上一动点,N是边BC的中点,则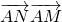 的最大值为________.
的最大值为________.

分析:由题意,得△ABC是以B为直角的直角三角形,因此建立如图直角坐标系,设M(x,y),可得向量
 和
和 的坐标,从而得到
的坐标,从而得到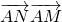 关于x、y的表达式,结合点M在△ABC内部或边界上运动,可得当点M与原点重合时
关于x、y的表达式,结合点M在△ABC内部或边界上运动,可得当点M与原点重合时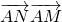 的最大值为
的最大值为 .
.解答:∵∠C=60°,AC=2,BC=1,

∴AB2=AC2+BC2-2AC•BCcos60°=3,得AB=

可得△ABC是以B为直角的直角三角形
因此,以C为原点,CB所在直线为x轴建立如图坐标系,
可得C(0,0),B(1,0),A(1,
 )
)∴BC中点N(
 ,0),得
,0),得 =(-
=(- ,-
,- )
)设M(x,y),得
 =(x-1,y-
=(x-1,y- )
)∴
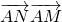 =-
=- (x-1)+(-
(x-1)+(- )(y-
)(y- )=-
)=- x-
x- y+
y+
点M在△ABC内部或边界上运动,当点M与原点重合时,-
 x-
x- y+
y+ =
= ,取得最大值
,取得最大值即
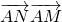 的最大值为
的最大值为
故答案为:

点评:本题给出直角三角形内的动点,求向量数量的最大值,着重考查了解三角形和平面向量的数量积公式等知识,属于中档题.

练习册系列答案
相关题目
 ABC,∠C=60°,AC=2,BC=1,点M是
ABC,∠C=60°,AC=2,BC=1,点M是 的最大值为__________。
的最大值为__________。 的最大值为 .
的最大值为 .