题目内容
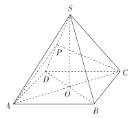
【题目】如图，几何体
中，
为边长为2的正方形，
为直角梯形，
，
，
，
，
．
（1）求证：
；
（2）求二面角
的大小．
【答案】（1）证明见解析；（2）
．
【解析】
试题分析：（1）证明：由题意得
，
平面
，
又
平面
，再由勾股定理得
平面
；（2）以
为原点，
，
，
所在直线分别为
，
，
轴建立如图所示的空间直角坐标系，平面
的法向量
，平面
的法向量为
．
试题解析： （1）证明：由题意得，，，
，
∴平面，∴，
∵四边形
为正方形，∴，
由
，
∴平面，∴，
又∵四边形
为直角梯形，
，
，
，
，
∴
，
，则有，∴，
由
，∴平面．
（2）由（1）知
，
，
所在的直线相互垂直，故以为原点，，，所在直线分别为，，轴建立如图所示的空间直角坐标系，
可得
，
，
，
，
，
，
由（1）知平面的法向量为，
∴
，
，
设平面的法向量为
，
则有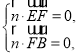
即
即
令
，则，
设二面角
的大小为
，
，
∵
，∴．
练习册系列答案
相关题目
【题目】某校高一年级开设了丰富多彩的校本课程，现从甲、乙两个班随机抽取了5名学生校本课程的学分，统计如下表．
甲 | 8 | 11 | 14 | 15 | 22 |
乙 | 6 | 7 | 10 | 23 | 24 |
用
分别表示甲、乙两班抽取的5名学生学分的方差，计算两个班学分的方差．得
______，并由此可判断成绩更稳定的班级是______班．
