Question

已知球与棱长均为2的三棱锥各条棱都相切，则该球的表面积为（　　）

• A、

  2

  3

  π
• B、2π
• C、2

  2

  π
• D、3π

Answer 1

分析：将三棱锥放入棱长为

2

的正方体，可得正方体的内切球恰好是与三棱锥各条棱都相切的球，根据三棱锥棱长算出正方体的棱长为

2

，由此算出内切球半径，用公式即可得到该球的表面积．

解答：解：将棱长均为2的三棱锥放入棱长为

2

的正方体，如图
∵球与三棱锥各条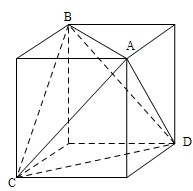棱都相切，
∴该球是正方体的内切球，切正方体的各个面切于中心，
而这个切点恰好是三棱锥各条棱与球的切点
由此可得该球的直径为

2

，半径r=

2

2

，
∴该球的表面积为S=4πr²=4π×(

2

2

)2=2π．
故选：B．

点评：本题主要考查了球的表面积公式的计算，多面体内切球和球的表面积公式等知识，构造正方体是解决本题的关键．