题目内容
【题目】已知圆M:x2+(y-2)2=1,Q是x轴上的动点,QA,QB分别切圆M于A,B两点。
(1)若Q(1,0),求切线QA,QB的方程;
(2)求四边形QAMB面积的最小值;
(3)若|AB|=![]() ,求直线MQ的方程。
,求直线MQ的方程。
【答案】(1)![]() 和
和![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】试题分析:(1)讨论直线的斜率是否存在,根据圆心到直线的距离等于半径求出直线的斜率;
(2)根据面积公式可知MQ最小时,面积最小,从而得出结论;
(3)根据切线的性质列方程取出MQ的值,从而得出Q点坐标,进而求出直线MQ的方程.
试题解析:
(1)设过点Q的圆M的切线方程为x=my+1,
则圆心M到切线的距离为1,
所以![]() ,所以m=
,所以m=![]() 或0,
或0,
所以QA,QB的方程分别为3x+4y-3=0和x=1。
(2)因为MA⊥AQ,所以S四边形MAQB=|MA|·|QA|=|QA|=![]() 。
。
所以四边形QAMB面积的最小值为![]() 。
。
(3)设AB与MQ交于P,则MP⊥AB,MB⊥BQ,
所以|MP|= 。
。
在Rt△MBQ中,|MB|2=|MP||MQ|,
即1=![]() |MQ|,所以|MQ|=3,所以x2+(y-2)2=9。
|MQ|,所以|MQ|=3,所以x2+(y-2)2=9。
设Q(x,0),则x2+22=9,所以x=±![]() ,所以Q(±
,所以Q(±![]() ,0),
,0),
所以MQ的方程为2x+![]() y+2
y+2![]() =0或2x-
=0或2x-![]() y-2
y-2![]() =0。
=0。

练习册系列答案
相关题目
【题目】2016年一交警统计了某段路过往车辆的车速大小与发生的交通事故次数,得到如下表所示的数据:
车速 |
|
|
|
|
|
事故次数 |
|
|
|
|
|
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)试根据(2)求出的线性回归方程,预测2017年该路段路况及相关安全设施等不变的情况下,车速达到![]() 时,可能发生的交通事故次数.
时,可能发生的交通事故次数.
(参考数据:![]() )
)
[参考公式: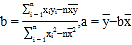 ]
]