题目内容
设y=f（x）在[0，+∞）上有定义，对于给定的实数M，定义函数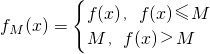
，给出函数f（x）=3-2x-x2，若对于任意x∈[0，+∞），恒有fM（x）=f（x），则M的最小值为________；M的最大值为________．
3 不存在
分析：先根据新定义的函数，将所求解的问题转化为求解恒成立问题，进而转化为求函数的最值问题，利用二次函数的单调性求解函数的最值，进而求出M的范围．
解答：由题意恒有fM（x）=f（x），需M≥f（x）对于任意x∈[0，+∞）恒成立
即需M≥f（x）的最大值，
由于f（x）=3-2x-x2=-（x+1）2+2
故f（x）在[0，+∞）上为减函数
故函数f（x）的最大值为f（0）=3
故M≥3，故M有最小值3，但无最大值
故答案为：3，不存在
点评：本题考查学生对新定义型问题的理解和掌握程度，理解好新定义的分段函数是解决本题的关键，不等式恒成立问题的解法，转化化归的思想方法
分析：先根据新定义的函数，将所求解的问题转化为求解恒成立问题，进而转化为求函数的最值问题，利用二次函数的单调性求解函数的最值，进而求出M的范围．
解答：由题意恒有fM（x）=f（x），需M≥f（x）对于任意x∈[0，+∞）恒成立
即需M≥f（x）的最大值，
由于f（x）=3-2x-x2=-（x+1）2+2
故f（x）在[0，+∞）上为减函数
故函数f（x）的最大值为f（0）=3
故M≥3，故M有最小值3，但无最大值
故答案为：3，不存在
点评：本题考查学生对新定义型问题的理解和掌握程度，理解好新定义的分段函数是解决本题的关键，不等式恒成立问题的解法，转化化归的思想方法
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设y=f（x）在[0，+∞）上有定义，对于给定的实数K，定义函数fK(x)=
，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）
|
A、K的最大值为
| ||
B、K的最小值为
| ||
| C、K的最大值为2 | ||
| D、K的最小值为2 |
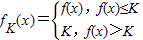，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）
，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）
