题目内容
设y=f（x）在[0，+∞）上有定义，对于给定的实数K，定义函数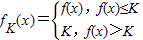
，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）A．K的最大值为
B．K的最小值为
C．K的最大值为2
D．K的最小值为2
【答案】分析：fK（x）的含义为：对于给定的实数K，函数值f（x）≤K时，保留原函数值，函数值f（x）＞K时，函数值变为K．
故fK（x）=f（x）时，f（x）≤K恒成立．所以本题转化为求f（x）的最大值问题．
解答：解：f（x）=2-x-x2在[0，+∞）上是减函数，故f（x）的最大值是f（0）=2，
由题意，f（x）≤K恒成立，只要K≥f（x）xax=2，即K≥2，所以K有最小值2
故选D
点评：本题为新定义问题，考查运用所学知识，分析问题解决问题的能力．
故fK（x）=f（x）时，f（x）≤K恒成立．所以本题转化为求f（x）的最大值问题．
解答：解：f（x）=2-x-x2在[0，+∞）上是减函数，故f（x）的最大值是f（0）=2，
由题意，f（x）≤K恒成立，只要K≥f（x）xax=2，即K≥2，所以K有最小值2
故选D
点评：本题为新定义问题，考查运用所学知识，分析问题解决问题的能力．
练习册系列答案
相关题目
设y=f（x）在[0，+∞）上有定义，对于给定的实数K，定义函数fK(x)=
，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）
|
A、K的最大值为
| ||
B、K的最小值为
| ||
| C、K的最大值为2 | ||
| D、K的最小值为2 |
，给出函数f（x）=2-x-x2，若对于任意x∈[0，+∞），恒有fK（x）=f（x），则（ ）
