题目内容
已知任意四边形ABCD中,E、F分别是AD、BC的中点.如图所示,求证:
思路分析:本题的证明方法比较多,可通过两个封闭图形得出![]() ,相加得出结论,也可以在平面内任选一点O,构成三角形,在三角形中利用向量加、减法的三角形法则找出关系式求解,也可以建立坐标系,利用向量的坐标运算求解.
,相加得出结论,也可以在平面内任选一点O,构成三角形,在三角形中利用向量加、减法的三角形法则找出关系式求解,也可以建立坐标系,利用向量的坐标运算求解.
证法一:∵E、F分别是AD、BC的中点,
∴![]() .
.
又![]() ,
,![]() ,
,
两式相加,得![]() 2,
2,
即![]() .
.
证法二:如下图所示,在平面内任取一点O.
∵E、F分别是AD、BC的中点,
∴![]() ,
,![]() .
.
∴![]()
=![]()
=![]() .
.
∴![]() .
.

证法三:建立直角坐标系,A(x1,y1),B(x2,y2),c(x3,y3),D(x4,y4).
则![]() =(x2-x1,y2-y1),
=(x2-x1,y2-y1), ![]() =(x3-x4,y3-y4),
=(x3-x4,y3-y4),
∴![]()
=(![]() ,
,![]() ).
).
又E(![]() ,
,![]() ),F(
),F(![]() ,
, ![]() ),
),
则![]() =(
=(![]() ,
,![]() ),
),
∴![]() =
=![]() .
.
方法归纳 利用平面向量基本定理证题的关键是选好与求证的结论相关的一组基底.基底选好后,平面内的任一向量都可用这组基底表示出来.一对相反向量的和等于零向量.在进行向量的加减运算时,可设法把向量转化成首尾相连的向量和的形式,有公共起点的向量的和差的形式等,以便于用向量的加减法法则去化简.

练习册系列答案
相关题目

 与
与 都是非零向量,则“
都是非零向量,则“ ”是“
”是“ ”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是
”的充要条件;②已知等腰△ABC的腰为底的2倍,则顶角A的正切值是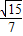 ;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设
;③在平面直角坐标系xoy中,四边形ABCD的边AB∥DC,AD∥BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为(0,-1);④设 ,
, ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足 与
与 不共线,
不共线, ⊥
⊥ ,|
,| |=|
|=| |,则|
|,则| •
• |的值一定等于以
|的值一定等于以 ,
, 为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)
为邻边的平行四边形的面积.其中正确命题的序号是 .(写出全部正确结论的序号)