题目内容
如图∠BAC=90°，等腰直角三角形ABC所在的平面与正方形ABDE所在的平面互相垂直，则异面直线AD与BC所成角的大小是_______．
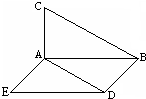
以A为坐标原点，以AE，AB，AC分别为x，y，z轴正方向建立空间坐标系，
∵∠BAC=90°，三角形ABC为等腰直角三角形，四边形ABDE为正方形
令AE=AB=AC=1
则D（1，1，0），B（0，1，0），C（0，0，1）
∴
=（1，1，0），
=B（0，-1，1）
设异面直线AD与BC所成角为θ
则cosθ=
=
故θ=60°
故答案为：60°
∵∠BAC=90°，三角形ABC为等腰直角三角形，四边形ABDE为正方形
令AE=AB=AC=1
则D（1，1，0），B（0，1，0），C（0，0，1）
∴
| AD |
| BC |
设异面直线AD与BC所成角为θ
则cosθ=
|
| ||||
|
|
| 1 |
| 2 |
故θ=60°
故答案为：60°
练习册系列答案
相关题目
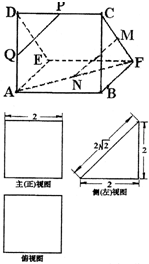
的平面角为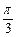
，AB⊥BC，BC⊥CD，
，BC在l上，
，若
，则AD的长为 .